Um corpo de massa ao ser largado de uma altura , apartir do repouso, num plano inclinado de um ângulo em relação a horizontal, atinge uma velocidade de módulo ao chegar na base do plano. Há atrito entre o corpo e a superfície do plano sendo o coeficiente de atrito cinético igual a . O mesmo corpo quando largado sob as mesmas condições em outro plano de mesma inclinação, mas sem atrito, atinge a base do plano com uma velocidade cujo módulo é o dobro da situação anterior. O valor de é igual a:

Vamos agora achar o trabalho total. É nessa parte que existe diferença entre as situações, vamos começar achando o trabalho para a situação sem atrito.

A única força que realiza trabalho é a força peso, então

Lembrando que ele é positivo porque a força está descendo, o deslocamento está na direção da força.

Temos na situação sem atrito

Vamos agora achar o trabalho total para a situação com atrito. Temos a força peso e o atrito atuando. O trabalho da força peso já achamos ali em cima. Vamos achar o trabalho da força de atrito

Ele é negativo porque a é contra o movimento. Precisamos agora achar e

Vamos começar fazendo o DCL, para encontrarmos a força normal. Vamos responder as perguntas do passo a passo para colocar as forças

1. A massa dele é considerada?

Sim, ele tem massa.

2. Ela esta encostada em alguma superfície?

Sim, o bloco está em contato com o chão.

3. Tem algum fio?

Não, não existe um fio atuando.

4. Tem mola?

Não, não existe mola atuando.

5. Tem atrito?

Sim, existe atrito.

Se a força de atrito não estivesse presente o bloco deslizaria pelo plano inclinado, logo ela é para a esquerda no . O DCL do bloco fica

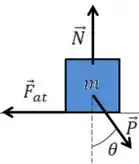
Já vimos que quando temos um plano inclinado, é mais fácil considerarmos a horizontal e vertical em relação a superfície inclinada, isso facilita nossas contas porque ele não tem movimento vertical em relação a essa superfície.

O ângulo fica na força peso com a vertical quando fazemos isso.

Fazendo o equilíbrio ao longo de

Devemos encontrar usando a “regra do COlado, SEparado”.

Como vamos achar ? Da um look na figura abaixo

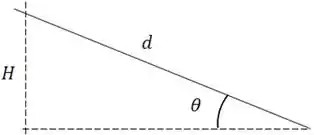
Podemos achar “Decompondo”

Recapitulando o que temos na situação onde ele desliza com atrito

Então

Essa questão está bem grande, vamos só dar uma olhada no que fizemos para não nos perdermos,

Estamos calculando o trabalho quando ele desliza com atrito pelo plano inclinado, estamos fazendo isso para usarmos o teorema trabalho – energia cinética.

Essa velocidade com atrito é a metade da velocidade sem atrito

Então

Substituindo na equação da velocidade com atrito

Ufa, questão gigante, complexa. Vou dar uma dica, é bem possível você ter se perdido ao longo da resolução, essa questão é bem difícil, mais difícil que algumas questões discursivas. É bom refazer essa questão algumas vezes olhando passo a passo para entender. Leia e releia que ela é difícil meeeesmo.