UFSC, Sem Campus, Física 1, Listas de Física 1 - UFSC - 7ª Lista, Questão 7
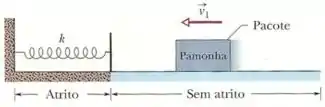
7) Um pacote com de pamonha, depois de deslizar ao longo de um piso com velocidade , choca-se com uma mola, comprimindo-a até ficar momentamente em repouso. Até o ponto em que o pacote entra em contato com a mola inicialmente relaxada o piso não possui atrito, mas enquanto o pacote está comprimindo a mola o piso exerce sobre o pacote uma força de atrito cinético de módulo . Se , qual é a variação do comprimento da mola entre o instante em que começa a ser comprimida e o instante em que o pacote para?
Passo 1
E aí! Suave na nave?! Tá difícil essa questão? Relaxa que a gente vai te ajudar!
Nesse problema temos uma caixa de massa que está indo em direção a uma mola com velocidade e após o contato com a mola, a caixa passa a possuir atrito com o solo de modulo .
Sabendo que a constante da mola é queremos saber a variação de que a mola comprime até a caixa parar.
Lembra como fazemos isso? 🤔
Nesse caso podemos usar o princípio da conservação de energia com perdas...
Podemos afirmar que a energia inicial do sistema é igual a energia final mais as perdas que ocorreram no caminho.
Inicialmente nosso sistema possui apenas energia cinética, então após o contato, a energia cinética é transformada em energia elástica na mola e ao mesmo tempo é perdida pelo atrito da caixa com o solo.
Preparado? Bora começar! 😉
Passo 2
Inicialmente temos que a energia cinética do sistema é dada por
A energia elástica na mola é dada por
E a energia perdida pelo atrito é igual ao trabalho realizado pela força de atrito, ou seja
Se a energia inicial é igual a energia final mais as perdas, então
Se , , e , então
Calculando as raízes desse polinômio, chegamos em
Portanto, a compressão da mola é dada por
O que achou? Foi de boa? Responde aí! 😊
