Um brinquedo consiste em um tubo inclinado de 30° em relação à horizontal contendo no fundo uma mola de constante elástica e uma bolinha de massa . Na posição , a mola está comprimida, e na posição a mola está relaxada e perde o contato com a bolinha. A mola é liberada arremessando a bolinha para fora do tubo. Fora do tubo, a bolinha descreve uma trajetória parabólica chegando a uma altura máxima . Suponha o atrito desprezível e responda às perguntas abaixo em função dos dados conhecidos do problema.

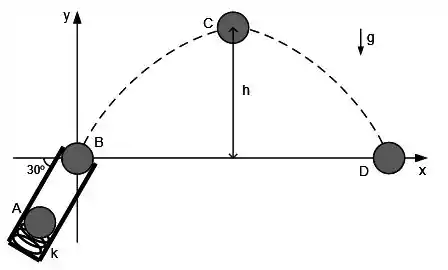
a) Usando conceitos de conservação de energia, determine o módulo da velocidade da bolinha quando ela passa pela origem do sistema de coordenadas da figura, ponto . Assuma que ela partiu do repouso.

b) Determine o tempo de permanência da bolinha no ar, entre os pontos e

c) Supondo a velocidade no ponto conhecida e utilizando a conservação de energia, escreva uma equação em função dos dados do problema que permita determinar a distância que a mola foi comprimida.

d) Considere agora que existe uma força de atrito do tubo que age na bolinha ao longo da distância enquanto ela vai da posição para a posição . Esta força de atrito varia linearmente com a distância, começando com o valor 0 (zero) na posição e chegando ao valor na posição . Calcule a variação da energia mecânica no trajeto.

b)

Considerando a origem o ponto , temos:

Mas no momento em que toca o eixo .

c)

Aplicando o principio da conservação da energia mecânica aos pontos e , temos:

Onde incluímos a energia potencial elástica .

d)

Podemos montar um gráfico onde a força de atrito é uma reta inclinada que parte de 0 e vai até . Do gráfico, encontramos a área da figura que é justamente o trabalho da força de atrito. Com isso temos que a variação da Energia mecânica é dada pela área embaixo da reta da força de atrito, ou seja, a fórmula da área de um triângulo: