UFMG, Sem Campus, Equações Diferenciais A, P3 - 2015.1, Questão 1
Encontre a transformada de Laplace de
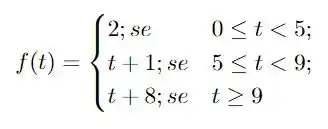
Passo 1
Oiie, tudo certinho?
O enunciado nos dá a seguinte função
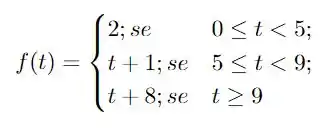
e pede para calcularmos a transformada de Laplace desta função! Esta é uma função com diferentes formatos para intervalos específicos. Funções desta forma podem ser reescritas utilizando a função de Heaviside definida como
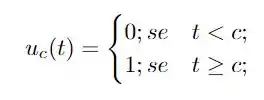
e, então vamos tentar reescrever a nossa função, daí aplicar a transformada sobre ela! Vem comigo!
Passo 2
Note que a nossa função é definida de forma que se , ou seja, se tivermos que , podemos escrever que
o termo está subtraindo para garantir que para , o seja cancelado e sobre apenas a função desejada no próximo intervalo! No entanto, isso sozinho não define a nossa função, precisamos dos outros intervalos! Agora, vamos analisar quando temos , temos que
e, finalmente, temos que para quando
Maravilha! A nossa função é dada então por
Maravilha! Mas porquê fazemos isso? Porquê a transformada de Laplace das funções heavisides são conhecidas! Vamos lá!
Passo 3
A transformada de uma função heaviside é tal que
Para a nossa função, temos que
como a transformada de Laplace é uma operação linear, podemos separar a expressão acima como
Ainda podemos expandir ainda mais para obter
Por simplicidade, vamos expandir um pouco mais os termos! Para obter
como podemos cancelar o termo de , obtendo
Estamos bem perto de podermos aplicar a nossa transformada, mas note que é necessário que a função esteja no formato . Vamos trabalhar a partir disso! Saca só!
Passo 4
Por exemplo, no terceiro termo temos que
como , precisamos que a função , seja escrita como . Para resolver isso, precisamos somar e subtrair me nossa transformada, de forma que
expandindo, temos que
Usando que
Temos então que a transformada de Laplace é simplesmente
E, aí está! A transformada de nossa função! A questão foi isso! Te vejo na próxima! Tchau Tchau!