UFMG, Sem Campus, Equações Diferenciais A, P3 - 2015.1, Questão 3
Resolva o PVI
Passo 1
Oiie, tudo certinho?
O enunciado nos dá o seguinte problema de valor inicial
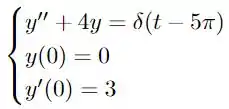
e, precisamos resolvê-lo. Existem diversas maneiras de fazermos isso, mas a ideia da prova é para que apliquemos transformada de laplace! E, também, isso será bastante conveniente devido que o termo não-homogêneo da equação diferencial é uma delta! Vamos lá!
Passo 2
Antes de começarmos vamos lembrar duas transformadas importantes, a primeira é tal que
em que . Também iremos precisar de
Se aplicarmos a transformada de Laplace em ambos os lados da equação diferencial, iremos obter que
aplicando a fórmula para a derivada da transformada de Laplace da derivada e da delta, temos que
Aplicando as condições iniciais, temos que
Vamos usar essa expressão para calcularmos a nossa função! Vem comigo!
Passo 3
Se isolarmos temos que
ou, simplesmente
Mas como achamos a nossa função ? Como temos que , portanto, temos que , sendo assim, podemos escrever
Para identificarmos as transformadas inversas, vamos relembrar algumas conhecidas! Vem comigo!
Passo 4
Temos as seguintes transformadas
e, também que
Se identificarmos em nossa expressão que , podemos dividir e multiplicar por , assim como , podemos finalmente escrever que
A questão foi isso! Te vejo na próxima! Tchau Tchau!