UTFPR, Sem Campus, Equações Diferenciais Ordinárias, Listas - Prof. Marcio Hiran Simões - Lista 1, Questão 2c
use a tabela de transformada de Laplace para calcular com
Passo 1
Fala galera, tudo bem com vocês? Vamos para mais uma questão!!! Nosso objetivo é usar a Tabela de Transformadas de Laplace para calcularmos com
Segue abaixo uma parte dessa tabela
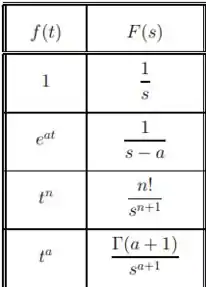
Passo 2
Queremos
Pela linearidade da transformada, temos:
Usando a tabela, obtemos que
Prontinho pessoal!! Finalizamos mais uma questão. Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊
Resposta
Exercícios de Livros Relacionados
Em cada um dos problemas de 21 a 24, encontre a transformada de Laplace da função dada.22. f ( t ) t , 0 ≤ t1 0 ,1 ≤ t∞
Em cada um dos problemas de 25 a 28, determine se a integral dada converge ou diverge.25. ∫ 0 ∞ t 2 + 1 - 1d t
Em cada um dos problemas de 1 a 4 , esboce o gráfico da função dada. Em cada caso, determine se f é continua, seccionalmente contínua, ou nenhuma das duas no intervalo 0 ≤ t ≤ 3 .2. f t = t 2 , 0 ≤ t
Em cada um dos problemas de 25 a 28, determine se a integral dada converge ou diverge.28. ∫ 0 ∞ e - t c o s td t
Em cada um dos problemas de 21 a 24, encontre a transformada de Laplace da função dada.21. f ( t ) 1 , 0 ≤ tπ 0 ,π ≤ t∞