Uma curva é a união de duas curvas e , onde é um segmento de reta e é uma porção da circunferência, conforme a figura. Pede-se:
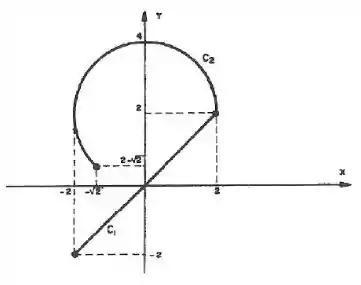
- Parametrize curvas e
- O comprimento total de .
Passo 1
é um segmento de reta.
Se observarmos a figura vemos que os pontos , e pertencem ao segmento. Assim, esse segmento nada mais que é que a reta , com :
Passo 2
Já é uma porção da circunferência de raio , centrada em .
A parametrização da circunferência nós já conhecemos. Assim:
Passo 3
Mas, precisamos notar que é apenas uma porção da circunferência, portanto, precisamos descobrir os limites do parâmetro .
Para isso, observamos que,no ínicio da curva (, temos o ponto e no final da curva , temos o ponto . Assim:
Então:
E
Então:
Assim:
Então, a parametrização de é:
Passo 4
Agora precisamos observar que , então, para calcular o comprimento total de , basta calcularmos o comprimento de e de e depois somar os dois.
Começando por :
Passo 5
Agora :
Passo 6
Para calcular os comprimentos precisamos apenas substituir nossos resultados em
Assim,
E
Passo 7
O comprimento da curva é, portanto: