Comprimento de Arco
Determine o comprimento da astroïde parametrizada por
(a)
(b)
(c)
(d)
(e)
Passo 1
Vou chamar a parametrização do astroïde de , beleza? Assim .
Então nessa questão precisamos calcular o comprimento de arco de entre os tempos e ! Aplicando a fórmula, temos
Então vamos calcular essa derivada! Com a regra da cadeia, vamos ter
Logo:
E como , isso vai dar
Passo 2
Excelente! Agora basta calcular a integral:
Vamos fazer
Então o comprimento é:
Passo 3
Temos que analisar o sinal de de a :
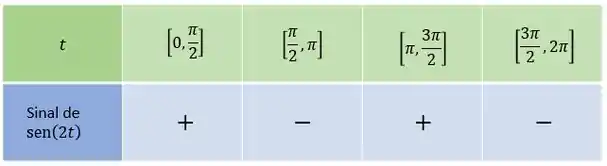
Logo, a integral pode ser dividida em:
Passo 4
Vou calcular os termos separadamente pra não ficar muito confuso, beleza?
Ufa! Então o comprimento é:
Aee, então a alternativa certa é a (c)!
Resposta
Alternativa (c)
Exercícios de Livros Relacionados
(a) Trace a epitrocoide com equações x = 11 cos t - 4 cos 11 t 2 y = 11 sen t - 4 sen 11 t 2 Qual intervalo do parâmetro fornece a curva completa?b) Use seu SCA para calcular o comprimento apr
Um barbante é enrolado ao redor de um círculo e então desenrolado, sendo mantido esticado. A curva traçada pelo ponto P no final do barbante é chamada involuta do círculo. Se o círculo tiver raio r e
Calcule o comprimento exato da curva polar: r = 2 c o s θ 0 ≤ θ ≤ π
51-54. Use uma calculadora ou um computador para encontrar o comprimento do laço, com precisão de quatro casas decimais. Se necessário, use um gráfico para determinar o intervalo de parâmetro.53. r =
Ao gravar apresentações ao vivo, os engenheiros de som usam um padrão de captação em forma de cardioide, pois ele suprime o barulho da audiência. Suponha que o microfone esteja colocado a 4m da frente