UFCG; Cálculo 2; Lista-3; questão 15a.
Determine o comprimento das curvas parametrizadas:
a) , ,
Passo 1
E aí galerinha, tudo beleza com vocês por aí?
A UFCG mandou essa questão para determinarmos o comprimento de curvas parametrizadas, mas o que isso significa??
Olha só, na imagem abaixo nós temos uma curva complexa em azul e para determinar o comprimento dessa curva, podemos dividir a curva em pedaços!!
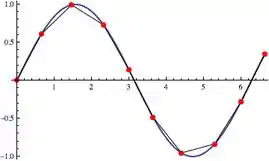
A ideia aqui é aproximar o comprimento da curva por um comprimento de segmento de reta que é bem mais simples de resolver, dá uma espiada na imagem abaixo!
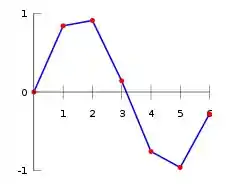
Ou sejaaa, podemos dizer que o comprimento do segmento de reta equivale a:
Logo, a soma de todos esses pedaços é o comprimento total , e assim obtemos a nossa relação de que é a integral da soma dos pedaços, sendo que cada pedacinho representa uma variação em e outra em , logo:
Passo 2
Agora nós já pegamos a ideia, vamos aplicar!
Primeiro vamos determinar a derivada de em relação à .
E a derivada de em relação à .
Belzinhaaa, agora é só substituir na equação (1) as derivadas de e em relação à e os limites de integração sendo .
Simplificando a raiz quadrada.
Logo, a integral equivale à:
Prontinho, encontramos o comprimento total da curva! Curtiu a resolução? Responde Aí ;)