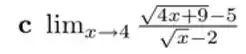
Passo 1
Começamos substituindo esse cara aí:
Indeterminação à vista! Vamos usar algum processo que elimine esse !
Passo 2
Temos duas raízes subtraídas de constantes, o que dá toda a indicação de usarmos o conjugado desses termos aí. Começamos multiplicando o denominador e o numerador pelo conjugado do termo de cima:
Passo 3
Agora multiplicamos o denominador e o numerador pelo conjugado do termo de baixo:
Passo 4
Agora a gente pode cortar o de cima com o de baixo e substituir o limite:
Resposta
Exercícios de Livros Relacionados
a) Use o gráfico de f x = 3 + x - 3 x para estimar o valor de lim x → 0 f ( x ) com duas casas decimais.b) Utilize uma tabela de valores de f ( x ) para estimar o limite com quatro casas decimais.c)
Estime o valor de lim x → 0 x 1 + 3 x - 1 fazendo o gráfico da função f x = x 1 + 3 x - 1 Faça uma tabela de valores de f ( x ) para x próximo de 0 e estime qual será o valor do limite.Use as propri
Calcule o limite, se existir.27) lim x → 9 x ² - 81 x - 3 ²
Ache o limite, se existir.underset(s - 7)(lim) (5 - sqrt(4 + 3 s))/(7 - s)
Calcule o limite, se existir.underset(h - 0)(lim) ((1)/((x + h)^2) - (1)/(x^2))/(h)