UTFPR - Sem Campus - Física 1 - Provas - Teste 9 -AV2 - 2022.2 - Questão 1 - Alternativa b
Um bloco de escorrega para baixo, a partir do repouso, em um plano inclinado que faz um ângulo de com a horizontal. O coeficiente de atrito cinético é de .
No instante em que o bloco percorre dois metros, qual a variação da energia térmica do sistema Terra-bloco?
Passo 1
Oiie, tudo bem?
Temos aqui um problema de mecânica bastante clássico, um bloco de massa , escorregando a partir do repouso em um plano inclinado em , que nem o desenho abaixo
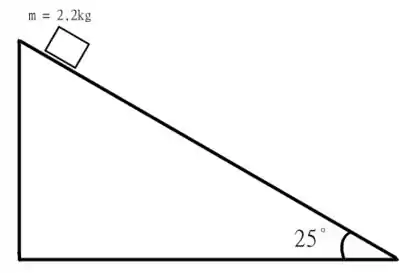
A superfície deste plano inclinado tem um coeficiente de atrito cinético . Então, precisamos para esta alternativa calcular a variação da energia térmica do sistema Terra-bloco após o bloco escorregar dois metros! Mas como isso? Essa não é uma questão de termodinâmica, certo? Mas não se preocupe, a variação da energia térmica de um sistema é simplesmente o trabalho realizado pelas forças resistivas presentes, em nosso caso, apenas a força de atrito! Então vamos utilizar essa informação para resolver nosso problema! Vamos lá!
Passo 2
O diagrama de forças construído na alternativa anterior é o seguinte
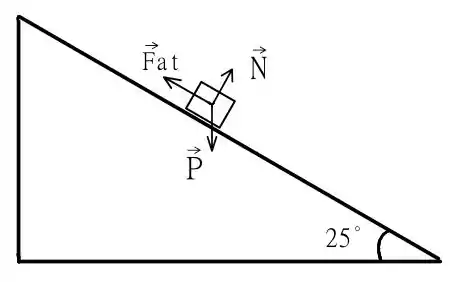
Assim como fizemos na alternativa anterior, os componentes da força peso são o seguinte
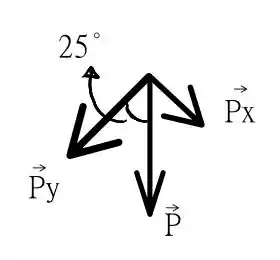
Como disse no passo , temos que a variação da energia térmica é o trabalho realizado pela força de atrito, ou seja, temos que
Vamos relembrar como calcular estas grandezas, belezinha?
Passo 3
Temos que a força de atrito cinético é uma força resistiva constante e que não depende do caminho tomado, portanto, podemos escrever que
em que é o vetor deslocamento, paralelo ao plano e a força de atrito, de forma que o nosso trabalho pode ser calculado simplesmente como
Temos que , como dito no enunciado, e temos como definição que
De forma que o módulo é simplesmente
Ou seja, o problema se resume em achar o módulo da força normal, já que nos foi dado . Vamos fazer isso agora!
Passo 4
Observando o nosso diagrama de forças resumido nos dois esquemas no passo , podemos identificar pela ausência de movimento perpendicular ao plano que
Tendo em vista a inclinação de nosso plano, temos que
De forma que temos
usando que , podemos escrever o módulo da força normal como
O módulo da nossa força de atrito é então dado como
Belezinha! Agora precisamos calcular o trabalho! E essa alternativa já era! Vamos lá!
Passo 5
Usando os dados do enunciado, temos que
em que é a aceleração da gravidade! Obtemos então que
Essa alternativa foi! Vamos para a próxima! Tchauzinho!