UFRJ, Física 1, Prova 1, 2016.1
Um skatista brinca em uma pista em forma de semicircunferência de raio R, com atrito desprezível, como mostrado na figura. Se o atleta sai do ponto A com velocidade , a altura h máxima que ele atinge, em relação à borda da pista, é:
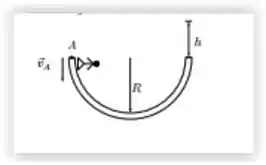
- 0
Passo 1
Como o atrito é desprezível, podemos utilizar a conservação da energia mecânica:
Utilizado o ponto inicial como referencial zero de altura e sendo o ponto de altura máxima, montamos:
Aqui, temos que ter uma sacada. No ponto de altura máxima, toda energia cinética de ponto A será convertida em potencial gravitacional e, assim, o skatista não terá velocidade. Continuando:
Resposta
Exercícios de Livros Relacionados
O cume do monte Everest está 8850m acima do nível do mar. (a) Qual seria a energia gasta por um alpinista de 90k g para escalar o monte Everest a partir do nível do mar, se a única força que tivesse q
Uma bola de 50g é lançada de uma janela com uma velocidade inicial de 8,0m / s e com um ângulo de 30 ° acima da horizontal. Usando a lei de conservação da energia, determine (a) a energia cinética da
Uma bola de neve de 1,50k g é atirada para cima em um ângulo de 34,0 ° com a horizontal e com uma velocidade inicial de 20,0m / s . (a) Qual é a energia cinética da bola? (b) De quanto varia a energia
Uma locomotiva com uma potência de 1,5M W pode acelerar um trem de uma velocidade de 10m / s para 25m / s em 6,0m i n . (a) Calcule a massa do trem. Determine, em função do tempo (em segundos), (b) a
b) Qual é a rapidez da bola ao chegar no chão