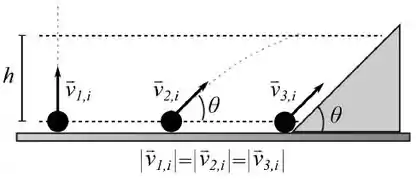
A figura mostra três partículas lançadas do mesmo nível com velocidades iniciais de mesmo módulo. A primeira é lançada verticalmente, a segunda fazendo um ângulo () com a horizontal e a terceira é lançada sobre um plano inclinado liso com ângulo de inclinação também igual a , como indica a figura. As três partículas passam por uma altura com rapidezes respectivas. Despreze a resistência do ar. Podemos afirmar que:

(A)

(B)

(C)

(D)

(E)

Nesse caso temos três lançamentos diferentes, entretanto com a mesma velocidade inicial.

A energia mecânica nesses três casos se conserva:

Nos três casos, eles apresentam a mesma energia inicial .

Isso porque os três são lançados com a mesma velocidade e por isso têm a mesma energia cinética:

Portanto, todos eles terão a mesma energia ao passarem pela determinada altura .

Essa energia estará dividida na forma de energia potencial gravitacional e energia cinética .

Como eles estão na mesma altura, a energia potencial gravitacional será igual entre eles. Então, sobra a mesma quantidade de energia na forma de energia cinética para os três casos. Portanto, eles tem a mesma velocidade ao passarem por aquela altura.

A conta de conservação de energia é a mesma para os três casos.

Ficamos com a alternativa (A).