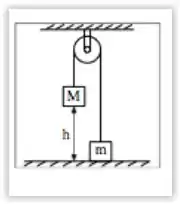
Considere o sistema de blocos de massas M=3 kg e m=1 kg que estão conectados por um cabo inextensível de massa desprezível que passa por uma polia fixa ao teto. O bloco de massa M é solto a partir do repouso desde uma altura h=2 m fazendo a polia de massa desprezível girar sem atrito até que o bloco toque o solo.
Seja a energia potencial gravitacional no instante inicial em que o bloco de massa M é solto, e Kf a energia cinética final do sistema no instante em que o bloco de massa M toca o solo. A fração de convertida em energia cinética desde o instante inicial até o instante final é:
(A) 1
(B) 2/3
(C) 1/2
(D) 1/6
(E) 1/3
Passo 1
Como sabemos que a energia mecânica se conserva, no caso desse problema a energia potencial se transforma em cinética e vice-versa.
Vamos primeiramente descobrir a energia potencial gravitacional inicial do sistema. Escolhendo o chão como referencial de altura nula, só temos o bloco M com energia potencial gravitacional de:
´
Como o sistema está em repouso, ou seja, não tem energia cinética, podemos dizer também que essa é a energia mecânica total do sistema:
Passo 2
Show!
Agora vamos descobrir a energia cinética final.
Uma boa maneira de fazer isso é calcular a energia potencial gravitacional final para descobrirmos o valor da energia cinética final.
No instante que o bloco M toca o solo, a energia potencial gravitacional do sistema é dada pela energia que o bloco obteve ao subir. Como trata-se de uma polia, podemos reparar que ele subiu que é o valor de .
Assim, .
Como temos a energia total do sistema e sabemos que ela se conserva, podemos achar o valor da energia cinética final:
Passo 3
O problema pede a fração de energia potencial gravitacional inicial convertida em energia cinética final. Então basta dividirmos o pelo que foram achados nos passos anteriores:
Resposta
(B) 2/3