A figura mostra um trilho perfeitamente liso contido em um plano vertical. Uma partícula é abandonada em repouso no ponto do trilho e desliza sobre ele sem nunca perder contato. A partícula passa pelos pontos , e e atinge o ponto , localizado na mesma altura que .
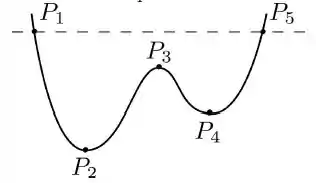
No percurso de a , a energia cinética é:
(a) Máxima em
(b) Mínima e igual em e
(c) Nula apenas em e
(d) Nula em , , , e
(e) Nula apenas em
Passo 1
A questão pergunta sobre a energia cinética nos pontos do trajeto. Além disso, temos que o trilho é perfeitamente liso (sem atrito), então vamos usar o fato que a energia mecânica se conserva:
A energia está dividida entre cinética () e potencial (), porém a soma delas () nunca vai mudar.
Quando a nossa partícula desce a rampa, ela vai perdendo altura (energia potencial) e ganhando velocidade (energia cinética), assim, temos energia potencial virando energia cinética, já quando ela sobe a rampa, ela ganha altura (energia potencial) e perde velocidade (energia cinética).
Passo 2
Na situação inicial (), a partícula está em repouso. Então sua energia cinética é zero. Por isso, sua energia mecânica total está apenas na forma de energia potencial gravitacional:
Agora, vamos comparar a energia em com a energia em , , e e analisar cada alternativa.
Passo 3
(a) energia cinética máxima em
O ponto de menor altura vai ser o ponto com energia cinética máxima.
Então, vai ser o ponto onde a partícula vai ter energia cinética máxima.
Letra (a) está errada.
Passo 4
(b) energia cinética mínima e igual em e
e estão à alturas (energias potenciais) diferentes. Então a velocidade (energia cinética) neles é diferente.
Como a altura em é menor, a velocidade nele é maior, logo:
Letra (b) está errada.
Passo 5
(a) energia cinética nula apenas em e
e estão a uma mesma altura, logo vão ter a mesma energia potencial:
Então, não sobra nenhuma parcela da energia mecânica na forma de energia cinética. Isso faz sentido, já que não tem como a partícula atingir uma altura maior da que ela já estava em (respouso).
Logo, a letra (c) está correta.
Mas vamos analisar as outras, porque a gente adora esse assunto de energia, né? hahah
Passo 6
(d) energia cinética nula em , , , e
Totalmente errada né?
Vimos que ao longo do trajeto a partícula ganha sim energia cinética.
Letra (d) está errada.
Passo 7
(e) energia cinética nula apenas em
A energia total em é:
A gente descobriu que a energia total é igual à potencial no início :
A altura de é menor que a de , então é menor que . Tudo isso, pra falar que a energia cinética não pode ser zero.
Além disso, a energia cinética em e é nula.
Letra (e) está errada.
Resposta
Letra (c)