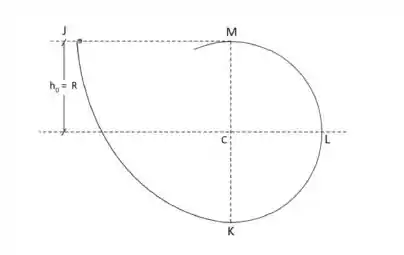
A figura mostra o perfil de um trilho contido no plano vertical, sendo o trecho circular, de centro e de raio . Umas esfera de pequenas dimensões é abandonada a uma altura acima do plano horizontal que contém o centro , passando a deslizar sobre o trilho com atrito desprezível. O módulo da força que o trilho exerce sobre a esfera no instante em que ele passa pelo ponto é
a)
b)
c)
d)
e)
f) nulo
Passo 1
Vamos desenhar a partícula no instante desejado:
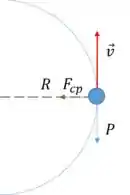
O módulo da força que o trilho faz na esfera é igual a normal e, portanto também é igual a força centrípeta.
Passo 2
Temos que encontrar o módulo da força centrípeta:
Ainda não sabemos a velocidade, certo? Como não há forças dissipativas, a energia mecânica é conservada:
Logo:
Resposta
(d)