Seja o salto de bungee jump mostrado ao lado nas seguintes três etapas: Posição – o saltador de massa se encontra em sua posição inicial com velocidade inicial igual a zero. Posição – o saltador caiu uma altura exatamente igual ao comprimento da corda relaxada. Após cair esta altura seu movimento passa também a estar sob ação da força elástica da corda. Posição – o saltador encontra sua posição de retorno com distensão máxima 𝑑 da corda e velocidade igual a zero. Sabendo que o comprimento da corda relaxada é e supondo sua constante elástica , despreze a resistência do ar e determine:
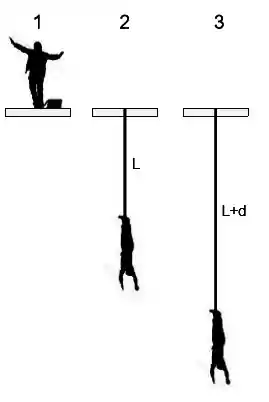
(a) A velocidade do saltador na posição .
(b) Sua velocidade máxima.
(c) A altura mínima da posição inicial para que o salto seja seguro.
Passo 1
(a)
O teorema do trabalho e energia cinética em e eixo positivo para baixo.
Passo 2
(b) O ponto de velocidade máxima ocorre quando
A conservação de energia mecânica total, no ponto em que .
Observe que esta equação é idêntica a equação da solução I portanto .
Passo 3
(c) A altura mínima corresponde à distância onde é a extensão máxima da corda que ocorre quando (desprezamos a altura do saltador que não foi informada nos dados da questão). Considerando o referencial com o eixo apontando positivo para baixo e no ponto em que .
Solução I: O teorema do trabalho e energia cinética.
A escolha do sistema de referências indica como solução correta , portanto, .
Resposta
(a)
(b)
(c)