Conservação de energia mecânica
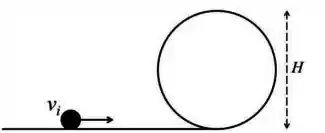
Um corpo puntiforme de massa e velocidade inicial se desloca sobre uma superfície horizontal sem atrito. Ao final dessa superfície existe um “loop” circular de diâmetro . Assumindo que não há atrito durante o “loop”, para que o corpo o complete, o módulo da velocidade deve ser tal que:
Passo 1
A grande sacada aqui é analisar a situação dinâmica do corpo na parte superior do loop, ou seja, la na pontinha superior do circulo.
A condição mínima pro loop é que naquele ponto a normal seja nula.
Assim, lembrando que a força resultante num movimento circular é uma força centrípeta:
Onde é a velocidade na parte superior do loop.
Assim, a nossa missão agora é achar , a velocidade na parte inferior do loop.
Passo 2
E como vamos achar isso? Usando a conservação da energia entre os dois pontos!!!!!
Fácil né? Bem, no ponto inicial só há energia cinética, já no ponto final a energia se divide em energia cinética e energia potencial.
Assim:
Agora, substituindo o valor de
Beleza? Bem, essa é velocidade mínima pro loop, então:
Resposta
e)