[ENUNCIADO COMUM ÀS QUESTÕES 1, 2 e 3 do 2°EE 2017.2]
Um esquiador de massa parte do repouso do ponto A, a uma altura acima da extremidade de uma rampa para saltos de esqui. Ele deixa a rampa no ponto B, fazendo um ângulo com a horizontal. O esquiador então atinge sua altura máxima no ponto C. Despreze os efeitos da resistência do ar e do atrito com a rampa. Dados: ; e .
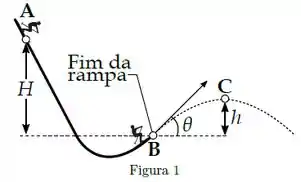
[Questão 1]
Considere as seguintes afirmações:
(I) A variação da energia potencial gravitacional do esquiador entre os pontos A e B é negativa.
(II) A variação da energia cinética do esquiador entre os pontos A e C é negativa.
(III) A variação da energia mecânica do esquiador entre os pontos B e C é positiva.
Das afirmações acima, são verdadeiras apenas:
(a) I
(b) II
(c) III
(d) I e II
(e) I e III
(f) II e III
(g) Todas
(h) Nenhuma
Passo 1
Todas as afirmações falam da variação de energia, seja mecânica, cinética ou potencial.
Então, vamos analisar o que acontece com a energia nesses pontos.
Primeiro de tudo, precisamos checar se a energia mecânica nesse sistema se conserva...
Temos duas forças atuando sobre o esquiador, a força peso e a força normal :
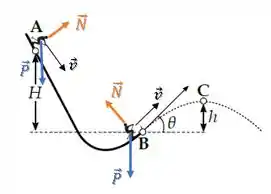
A força peso é uma força conservativa, ela não retira energia do sistema. Já a força normal não é conservativa.
Entretanto, dá uma olhada na direção da velocidade do esquiador. Como a força normal é perpendicular ao deslocamento em todo o trajeto, essa força não realiza trabalho... não retira energia do sistema.
Então, a energia mecânica se conserva!
Essa análise inclui a trajetória após a rampa, pois o esquiador estará sujeito apenas à força peso.
Passo 2
A afirmação 1 fala que a variação de energia potencial gravitacional entre A e B é negativa, ou seja que a energia diminui.
Energia potencial gravitacional é dada por:
Onde e são a massa e a gravidade, respectivamente, e é uma altura a partir de um referencial que escolhemos. Isso significa que quanto maior a altura, maior a energia potencial gravitacional.
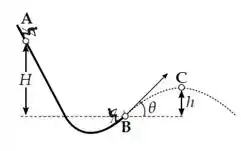
Como a altura de A é maior que a altura de B, a energia potencial gravitacional em A também será maior que em B:
Ou seja, a energia potencial realmente diminuiu e a variação é negativa:
A afirmação (I) está correta.
Passo 3
(II) A variação da energia cinética do esquiador entre os pontos A e C é negativa.
A afirmação (II) diz que a energia cinética em A é maior que em C.
No fim das contas, a energia cinética depende apenas da velocidade do esquiador.
Então fica bem simples de compará-las. O esquiador está em repouso em A, então sua energia cinética nesse ponto é nula:
Já em C, o esquiador está com uma certa velocidade, então, sua energia cinética diferente de zero:
Logo, a variação de energia cinética foi positiva (aumentou) entre os pontos A e C:
OBS: Se a rampa tivesse uma inclinação de , o esquiador realizaria um lançamento vertical. Assim, ele alcançaria a mesma altura que o ponto A, tendo sua velocidade nula nesse ponto de altura máxima C, já que não existiria uma componente horizontal da velocidade.
A afirmação (II) está incorreta.
Passo 4
(III) A variação da energia mecânica do esquiador entre os pontos B e C é positiva.
Começamos a questão vendo que a energia mecânica se conserva, inclusive após a rampa, quando há apenas a força peso (conservativa) no esquiador.
Então, a variação de energia mecânica é nula em quaisquer dois pontos:
A afirmação (III) está incorreta.
Resposta
Letra (a)