Uma máquina de Atwood consiste em duas massas, e e uma polia sem massa e sem atrito. Partindo do repouso, a rapidez das duas massas chega ao final de . Neste tempo, a energia cinética do sistema atinge e cada massa terá se deslocado uma distância de . Determine os valores de e .

Vamos começar, relacionando as duas incógnitas, e , à energia cinética que é fornecida quando elas estão com a seguinte velocidade:

Vamos lá!

Como temos duas incógnitas (e ) precisamos de duas equações para montar um sistema.

Para encontrarmos essa nova equação podemos fazer de dois jeitos. Vou mostrar os dois aqui.

A primeira maneira é usando conservação da energia mecânica.

Mas o exercício diz que ambas as massas partem do repouso, então:

Além disso, o enunciado também nos diz que

Para analisarmos as energias potenciais vamos pensar no seguinte: considerando o zero de energia potencial na posição inicial de 2 e sabendo que ambas as massas se deslocam por 6 metros, temos:

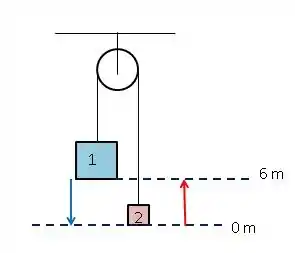
Então:

Assumimos que , então:

E

Como , temos:

Substituindo isso na equação de conservação de energia mecânica:

Mas,

Logo:

Resolvendo isso daí:

Show, temos então essas duas equações:

Resolvendo esse sistemas, encontramos:

Maravilha!! Essa foi a primeira form de acharmos as massas, vou mostrar mais uma.

Vamos usar a segunda lei de Newton, para achar a segunda relação que falta entre e . Sabemos que a aceleração é a mesma para os dois blocos, certo? Só que enquanto um fio sobe, o outro desce. Por isso, consideremos o sentido positivo para cima:

Temos então, o seguinte sisteminha, onde , e são respectivamente o peso do bloco de massa , a força de tração e o peso do bloco de massa .

Somando então as duas equações do nosso sistema, chegamos a:

Só que tem um porém. A questão diz que as massas chegaram a ao final de . Ou seja elas foram aceleradas. Encontramos, o meio de achar a aceleração :

Usando a fórmula da velocidade para o movimento uniformemente acelerado, partindo do repouso temos que:

Voltemos à fórmula anterior:

Tínhamos obtido antes, que:

Opa! Mas que beleza! Só susbtituir agora .

E como: