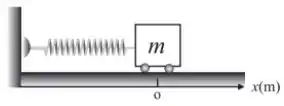
. Uma mola tem uma extremidade fixa em uma parede vertical e a outra num carrinho de massa , que movimenta-se como uma partícula numa superfície horizontal sem atrito, sujeita a uma força elástica dada por . Se o carrinho passa pela posição com velocidade , sua velocidade escalar ao passar pela posição , em metros por segundo, é:

Vamos detonar com essa juntos!

Para encontrar essa velocidade, vamos fazer um caminho onde vamos usar a conservação de energia, dada por:

Onde é a energia cinética do carrinho e é a energia potencial elástica relacionada a mola, assim:

Onde o instante inicial é em e o final é em que é o que nos interessa. Então a energia potencial inicial é zero, assim:

Na nossa expressão temos a constante elástica que podemos encontrar o valor dela lembrando que a força que uma mola realiza em um corpo é dada por:

Comparando com a força que o enunciado nos deu, temos que .

Com isso a gente pode isolar e calcular seu valor.