UFPE – Física 1 2019.2 – Prova Final– Questão 6
Um bloco de massa encontra-se em um plano inclinado de um ângulo , com e . Uma mola de constante elástica tem uma extremidade presa à parte superior do plano e a outra presa ao bloco. Inicialmente o bloco está parado e a mola está relaxada. Não há atrito no problema e . O bloco desce ao ser liberado. Quando o bloco está a uma distância da posição inicial (medida ao longo do plano inclinado), qual é a sua energia cinética?
Passo 1
Fala galera, tudo bem? Vou ajudar você a resolver essa questão! Vamos lá?
Vamos começar com um desenho:
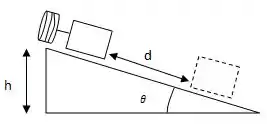
No instante inicial o bloco apenas tem energia potencial gravitacional, ao ser solta da altura , ela adquire não só energia cinética, como também energia potencial elástica. Então para determinar a energia cinética desse bloco, vou usar aqui a lei de conservação de energia, já que o plano não tem atrito.
Passo 2
A altura inicial vai ser o cateto oposto do triângulo formado pela distância , pela altura e pela base do plano inclinado. Em termos do ângulo de inclinação do plano, a altura está relacionada com o seno desse ângulo:
E assim a energia potencial gravitacional inicial é:
Passo 3
Agora, ao liberar o bloco, ele ganha energia potencial elástica e cinética e essa última é o que queremos descobrir. Então, por conservação de energia temos que toda a energia gravitacional foi convertida em cinética e elástica:
Alternativa (b).
Beleza?
Pronto pra próxima questão? =)
Resposta
Alternativa (b).