Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Conservação da Energia Mecânica

Ver Teoria
Exercício 381234567891011121314151617181920212223242526272829303132333435363739404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Um bloco de massa M encontra-se em repouso sobre uma superfície horizontal sem atrito, preso a um suporte rígido, por uma mola de constante k , conforme ilustrado abaixo. Uma bala de massa m e velocidade v atinge o bloco e permanece dentro do bloco.

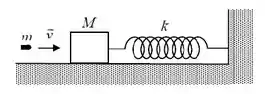
Determine, em termos de M ,   k ,   m   e   v , a amplitude do movimento harmônico simples resultante é:

  1. x m = m v k m + M  

  2. x m = M 2 v k m + M

  3. x m = ( m + M ) v k m

  4. x m = K M v m + M

  5. x m = m 2 v k m + M

Passo 1

Calcularemos a amplitude do MHS.

Encontrando a velocidade imediatamente após a colisão da bala com o bloco.

Conservando o momento linear, teremos:

p i = p f ⇒ m v = M + m v f ⇒ v f = m v M + m

A amplitude do MHS corresponde à compressão máxima da mola. Neste momento, o bloco está parado, ou seja, sua energia cinética é nula. Utilizando estas informações, teremos:

Início (imediatamente após a colisão) –   x = 0 :

K 0 = 1 2 m + M v f 2     e     U 0 = 0

Fim (No momento de compressão máxima da mola) –   x = x m :

K x m = 0     e     U x m = 1 2 k x m 2

Conservando a energia, teremos:

1 2 m + M . m v M + m 2 = 1 2 k x m 2 ⇒ x m =   m + M k . m v M + m

Assim,

  x m = m v k M + m

Resposta

L e t r a   A

Exercícios de Livros Relacionados

O cume do monte Everest está 8850m acima do nível do mar. (a) Qual seria a energia gasta por um alpinista de 90k g para escalar o monte Everest a partir do nível do mar, se a única força que tivesse q
Uma bola de 50g é lançada de uma janela com uma velocidade inicial de 8,0m / s e com um ângulo de 30 ° acima da horizontal. Usando a lei de conservação da energia, determine (a) a energia cinética da
Uma bola de neve de 1,50k g é atirada para cima em um ângulo de 34,0 ° com a horizontal e com uma velocidade inicial de 20,0m / s . (a) Qual é a energia cinética da bola? (b) De quanto varia a energia
Uma locomotiva com uma potência de 1,5M W pode acelerar um trem de uma velocidade de 10m / s para 25m / s em 6,0m i n . (a) Calcule a massa do trem. Determine, em função do tempo (em segundos), (b) a
b) Qual é a rapidez da bola ao chegar no chão