UFSC, Sem Campus, Física 1, Listas de Física 1 - UFSC - 7ª Lista, Questão 2
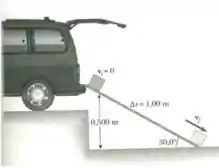
2) Uma caixa de desliza rampa abaixo em um galpão de carga. A rampa tem de comprimento e está inclinada a um ângulo de , como mostrado na figura abaixo. A caixa começa do repouso no topo e sofre a ação de uma força de atrito constante de módulo . Calcule a velocidade escalar da caixa quando ela atinge a parte mais inferior da rampa, pelos métodos de conservação de energia.
Passo 1
Fala aí, querido!! Tudo certinho? Bora resolver esse probleminha? 😉
Nesse problema temos uma caixa de massa que desliza sob uma rampa de que está a de inclinação.
Sabendo que a força de atrito entre a caixa e a rampa tem módulo queremos saber qual é a velocidade da caixa no ponto mais baixo da rampa.
Parece dificil? 🤔
Nesse caso podemos usar o princípio da conservação de energia...
Ou seja, a energia interna do sistema é igual a soma da energia gasta com a energia final.
Inicialmente temos apenas energia potencial gravitacional
A energia gasta no sistema é decorrente da força de atrito e podemos obtê-la a partir do trabalho da força
E a energia final da caixa é unicamente cinética
Sacou a ideia? 👀
Passo 2
Montando a equação do problema, temos
Isolando , temos
Se , , e , temos
Sacou como faz? Responde Aí! 😉
