UnB - Física 1 - Listas -Lista 8: Conservação de Energia - Questão 7
Um pequeno bloco de massa desliza em um círculo vertical de raio por uma faixa circular. Não existe atrito entre a faixa e o bloco. Enquanto o bloco se encontra no ponto mais baixo de seu caminho, a força normal que a faixa exerce no bloco tem módulo de . Encontre o módulo da força normal que a faixa exerce no bloco quando este está localizado no ponto mais alto do caminho.
Passo 1
Fala aí, beleza?? Vamos para mais uma questãozinha!
Temos a seguinte situação um bloquinho desliza sobre uma faixa circular sem atrito. Sabemos que no ponto mais baixo da trajetória a força normal é de e temos que encontrar quanto vale a força normal no ponto mais alto da trajetória.
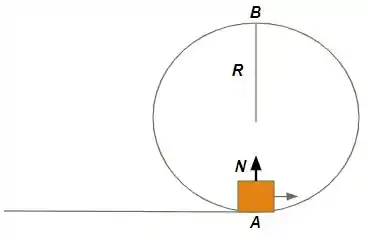
Como podemos começar a resolver essa questão???
Passo 2
Sendo o ponto mais baixo da trajetória e o ponto mais alto, vamos começar analisando as forças presentes no bloquinho.
No ponto :
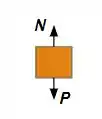
Pela segunda lei de Newton:
Como se trata de um movimento circular a aceleração em questão será a aceleração centrípeta.
Substituindo com os dados do enunciado:
Então encontramos a velocidade do bloquinho no ponto mais baixo da trajetória, agora só falta encontrar a velocidade na parte mais alta da trajetória.
Passo 3
Utilizando a conservação de energia:
Como não temos nenhuma força dissipativa . E, a energia potencial no ponto também é , já que o ponto mais baixo da trajetória se encontra na superfície do nosso referencial.
Assim,
Sendo :
Ótimo! Encontramos a velocidade no ponto mais alto da trajetória e agora vamos utilizar isso para descobrir a força normal nesse ponto.
Passo 4
No ponto :
Utilizando novamente a segunda lei de Newton:
Como as duas forças no ponto mais alto apontam para o centro da trajetória circular, ambas serão positivas e se somam.
Substituindo com os dados do enunciado e sabendo que :
Conseguimosssss! Espero que lágrimas não tenham caído no caminho hahaha
Bora treinar mais?!