Imagine que você deixa cair (abandonando) um objeto de massa de uma altura de metros. Determine a velocidade desse objeto ao tocar o solo. Despreze a resistência do ar e considere .
(a)
(b)
(c)
(d)
(e)
Passo 1
Vamos entender o que está acontecendo!
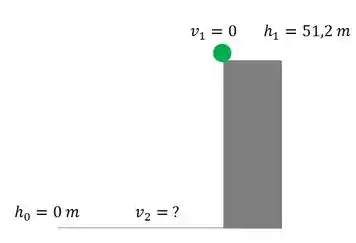
Como que a gente acha a velocidade 2 da bolinha?
Acompanha aqui comigo!
Passo 2
Como não tem atrito com o ar, temos que não exitem forças dissipativas roubando energia do nosso sistema. Então a energia mecânica se conserva.
Lá em cima, a energia cinética é pois a bolinha foi solta do repouso, logo só temos energia potencial gravitacional.
Já, quando ela chega no chão, a altura é zero, e a energia potencial é nula. Temos somente a cinética nesse caso.
Então:
Resolvendo essa continha:
Show??
Resposta
Alternativa (c)
Exercícios de Livros Relacionados
O cume do monte Everest está 8850m acima do nível do mar. (a) Qual seria a energia gasta por um alpinista de 90k g para escalar o monte Everest a partir do nível do mar, se a única força que tivesse q
Uma bola de 50g é lançada de uma janela com uma velocidade inicial de 8,0m / s e com um ângulo de 30 ° acima da horizontal. Usando a lei de conservação da energia, determine (a) a energia cinética da
Uma bola de neve de 1,50k g é atirada para cima em um ângulo de 34,0 ° com a horizontal e com uma velocidade inicial de 20,0m / s . (a) Qual é a energia cinética da bola? (b) De quanto varia a energia
Uma locomotiva com uma potência de 1,5M W pode acelerar um trem de uma velocidade de 10m / s para 25m / s em 6,0m i n . (a) Calcule a massa do trem. Determine, em função do tempo (em segundos), (b) a
b) Qual é a rapidez da bola ao chegar no chão