Uma granada explode em três fragmentos iguais de massa . Após a explosão, o primeiro fragmento vai para o oeste e os outros dois nas seguintes direções: ao norte e ao sul, ambos em relação à direção leste. A energia cinética total liberada foi de . Quais são os módulos das velocidades iniciais dos 3 fragmentos, logo após a explosão?
Passo 1
Fala galera, tudo bem? Essa questão parece complicada, mas estou aqui para te ajudar! Vamos resolver juntos? Vamos fazer um desenho dessa situação!
Digamos que a granada (ponto preto grande) estivesse na origem. Sendo assim um dos fragmentos está na direção oeste (em vermelho, na direção negativo de ), o outro está a ao norte (ou seja acima do eixo , está em azul) e o último está a ao sul (ou seja, abaixo do eixo , está em verde).
Então um esquema com essas coisas fica mais ou menos assim:
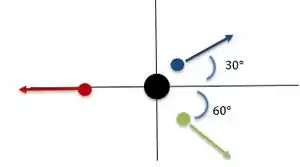
A gente pode atribuir vetores velocidades a esses fragmentos. A ideia aqui é usar a conservação de energia + a conservação de momento linear para achar essas velocidades. Beleza?

Passo 2
Vamos agora identificar os vetores velocidades desse problema. Lembrando o desenho que fiz ali em cima:
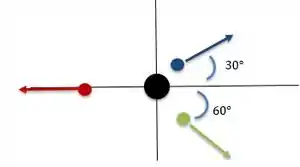
Vamos começar pelo fragmento vermelho. Ele está na direção de negativo, e digamos que ele tem uma velocidade depois da explosão, então o vetor que vai representar ele é:
Beleza?
Agora o fragmento azul:
Ele está acima o eixo , no primeiro quadrante, então as componentes x e y desse vetor são positivas. Dizendo que ele assume uma velocidade depois da explosão, o vetor que representa ele é:
E por fim o fragmento verde:
Ele está abaixo o eixo , no quarto quadrante, então a componente x é positiva, mas a y é negativa!
Dizendo que ele assume uma velocidade depois da explosão, o vetor que representa ele é:
Tudo bem até aqui?
Passo 3
Agora vou usar a conservação de momento linear! O momento linear TOTAL do sistema deve ser SEMPRE conservado! Como tudo estava em repouso, o momento linear total inicial é zero!
E o final? Bom, ele é a soma vetorial dos momentos individuais de cada fragmento! (lembra que fazer uma soma vetorial é somar componente a componente)
O momento linear é o produto da massa pela velocidade, assim os momentos dos fragmentos são:
E o momento linear final total é a soma de todos esses momentos:
Sabemos que o momento se conserva, daí:
Então precisamos somar componente a componente e igualar a zero! Teremos um sistema de duas equações e três incógnitas! Saca só:
Da equação em podemos determinar em função de :
E agora da equação em a gente pode ter em função de :
Bom, precisamos de outra equação!
O momento sempre se conserva! Mas aqui a ENERGIA TAMBÉM!
A outra equação que precisamos é a equação e conservação de energia!

Passo 4
A energia total liberada foi de , então quer dizer que a energia cinética total dos fragmentos é igual a energia liberada!
Assim temos que:
Deixando de uma forma mais simpática temos o seguinte:
A massa de cada fragmento é igual a , então já vou calcular o valor do lado esquerdo dessa equação:
Mas do passo anterior temos que:
Então vou substituir essas duas velocidades na equação da energia e ficar com uma equação apenas em :
Oba!
E agora podemos achar as outras velocidades:

Pronto! Terminamos!
Espero ter te ajudado!