Escrever a Tag aqui (nome do capítulo IGUALZINHO), Outra tag, Mais uma tag
Dois blocos, de massas M = 3,0 kg e m = 1,0 kg, são inicialmente mantidos em repouso sobre uma superfície horizontal, comprimindo uma mola ideal. Ao serem simultaneamente liberados da mola, cada bloco viaja para um lado e sobe uma rampa inclinada. Considere que a velocidade do bloco de massa M logo após ser liberado é V = 3,0 m/s. Despreze todos os atritos e use
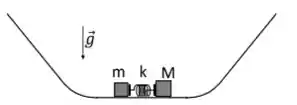
Qual é a variação da energia potencial elástica (em módulo) antes e depois dos blocos serem liberados?
a) 10 J
b) 12 J
c) 24 J
d) 28 J
e) 36 J
f) 42 J
g) 54 J
h) 58 J
Passo 1
Pela conservação de Energia, a gente sabe que toda Energia Cineética desses blocos irão se converter em Energia Potencial Elástica, né? Show, então temos:
Acabamos!
Resposta
g) 54 J
Exercícios de Livros Relacionados
O cume do monte Everest está 8850m acima do nível do mar. (a) Qual seria a energia gasta por um alpinista de 90k g para escalar o monte Everest a partir do nível do mar, se a única força que tivesse q
Uma bola de 50g é lançada de uma janela com uma velocidade inicial de 8,0m / s e com um ângulo de 30 ° acima da horizontal. Usando a lei de conservação da energia, determine (a) a energia cinética da
Uma bola de neve de 1,50k g é atirada para cima em um ângulo de 34,0 ° com a horizontal e com uma velocidade inicial de 20,0m / s . (a) Qual é a energia cinética da bola? (b) De quanto varia a energia
Uma locomotiva com uma potência de 1,5M W pode acelerar um trem de uma velocidade de 10m / s para 25m / s em 6,0m i n . (a) Calcule a massa do trem. Determine, em função do tempo (em segundos), (b) a
b) Qual é a rapidez da bola ao chegar no chão