Um sistema massa-mola horizontal executa um movimento harmônico simples com amplitude . Quando o deslocamento da massa é , qual das expressões abaixo representa corretamente a rapidez da massa em termos de sua rapidez máxima? Dica: use a conservação da energia.
(A) (B)(C) (D)v=3 (E)
Passo 1
Fala aí galerinha? Tudo bem com vocês? Bora pra cima! A ideia da questão é que temos que pegar a velocidade no meio do movimento. Ou seja, precisamos entender como a velocidade se comporta durante o movimento do sistema. E quem melhor nos dizer como as coisas se comportam, do que uma equação bem montada, não acha? HAHAHA. Pra isso, vou esquematizar 3 situações. Se liga;
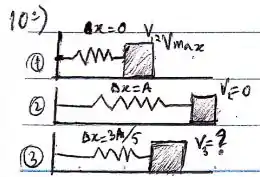
No primeiro momento eu já tenho o sistema em movimento pleno. Também tenho uma deformação na mola , no entanto a velocidade do bloco é máxima. Para o segundo momento, tenho a mola totalmente esticada, ou seja, chegou na sua amplitude máxima . Nesse momento, ele está na iminência de ir para a direção contrária, e sua velocidade é . No terceiro momento, que é o que nos interessa, a deformação da mola está em . Queremos descobrir sua velocidade. No próximo passo eu te mostro 😊

Passo 2
Então, temos 3 momentos diferentes pra trabalhar aqui, mas eles têm uma coisa em comum. Em todos eles, a soma das energias potenciais e cinéticas é a mesma. Isso pelo principio de conservação de energia. Então, significa que para esses três momentos:
(1)
e são respectivamente energia cinética e potencial. E as letrinhas pequeninas ali em baixo “ e ” indicam os 3 estados do esqueminha, perfeito? Então bora lá. Abrindo a primeira parte da equação, temos:
Mas, no primeiro momento, sabemos que , já que tomamos como referencia o inicio do movimento. Logo:
Para a segunda parte:
Porém, a velocidade final é igual a 0, portanto:
Para a terceira parte:
Aquele é justamente a variável que a gente quer. Bora pro próximo passo preparar pra arrematar a questão?
Passo 3
Juntando as equações (2), (3) e (4) nos moldes da equação (1), temos:
Aqui não precisamos nos assustar com essa equação um tantinho grande. Vamos resolver ela em partes... confia que vai dar certo 😊. Primeiro relacionando a primeira parte com a terceira, temos:
Desenvolvendo isso:
Belezinha, mas veja só: Relacionando a primeira parte com a terceira temos:
Podemos jogar essa relação dentro da nossa equação (5). Então temos:
Agora é só resolver e isolar . Logo:
Multiplicando por 2:
Dividindo pela massa dos dois lados:
Achaaaamos! Resposta correta é o item c).

E é isso! WE DID IT!!! Se ficou alguma dúvida, quer dar alguma sugestão ou reportar algum erro, manda um feedback pra gente! Vamos adorar ajudar você
Resposta
Alternativa c)