[ENUNCIADO COMUM ÀS QUESTÕES 1, 2 e 3 do 2°EE 2017.2]
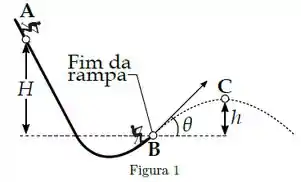
Um esquiador de massa parte do repouso do ponto A, a uma altura acima da extremidade de uma rampa para saltos de esqui. Ele deixa a rampa no ponto B, fazendo um ângulo com a horizontal. O esquiador então atinge sua altura máxima no ponto C. Despreze os efeitos da resistência do ar e do atrito com a rampa. Dados: ; e .
[Questão 2]
O módulo da velocidade do esquiador em B é:
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
Passo 1
Sempre que não tivermos muitas informações sobre cinemática, como acelerações, tempo de duração do movimento, etc, é um bom indicativo de que o caminho da questão seja por análise da energia.
Como temos informações sobre o ponto A, podemos usar esse ponto e compará-lo com B.
Como temos a diferença de altura entre os dois pontos , além da massa do patinador, um bom caminho para achar o módulo da velocidade em B é através da conservação da energia mecânica.
Mas, para isso, precisamos checar se a energia mecânica nesse sistema se conserva...
Passo 2
Temos duas forças atuando sobre o esquiador, a força peso e a força normal :
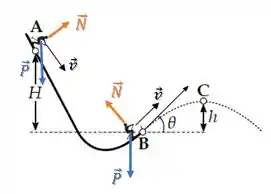
A força peso é uma força conservativa, ela não retira energia do sistema. Já a força normal não é conservativa.
Entretanto, dá uma olhada na direção da velocidade do esquiador. Como a força normal é perpendicular ao deslocamento em todo o trajeto, essa força não realiza trabalho... não retira energia do sistema.
Então, a energia mecânica se conserva!
Passo 3
Agora, podemos usar a conservação da energia mecânica para achar a velocidade do esquiador em B.
No ponto A, o esquiador está em repouso, logo sua energia cinética é zero, restando apenas a energia potencial :
Vamos colocar o nosso referencial de altura zero no ponto B, então o ponto A se encontra à uma altura :
No ponto B, o esquiador está a uma altura zero, segundo o nosso referencial, então sua energia potencial é nula. Porém, ele tem uma energia cinética associada à sua velocidade:
Passo 4
Juntando as informações na conservação da energia mecânica, temos:
Substituindo os valores:
Achamos a velocidade do esquiador em B e ficamos com a alternativa (c).
Resposta
Letra (c)