Um projétil é lançado do solo numa direção que faz um ângulo com a horizontal. Desprezando-se a resistência do ar e tomando o zero da energia potencial no nível de lançamento, a razão entre a energia cinética e a energia mecânica do projétil quando ele atingir a altura máxima é
(a)
(b)
(c)
(d)
(e)
Passo 1
Se liga! Vamos começar fazendo uma pequena decomposição da velocidade de acordo com o que foi informado no enunciado.
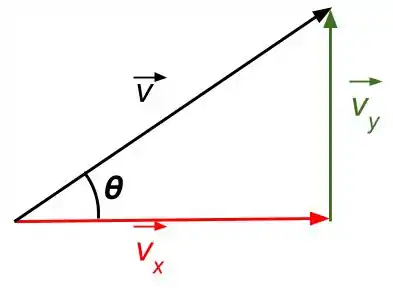
Repare que podemos escrever que
Passo 2
Levando em consideração que no ponto mais alto da trajetória não temos velocidade na direção , e que em todo o percurso a velocidade na direção é constante, podemos então escrever que a energia cinética no ponto mais alto é
Passo 3
Tendo em vista que no início do lançamento toda energia que temos é cinética e que a energia deve ser conservada. Podemos escrever que a energia mecânica total em qualquer instante é
Como ele pede , temos
Portanto a alternativa correta é a letra (a).