Um carrinho de montanha-russa, de , parte do repouso de uma altura acima da base de uma laço de de diâmetro. Se o atrito é desprezível, determine a força para baixo exercida pelos trilhos sobre o carrinho, quando este está no topo do laço, de cabeça para baixo.

Passo 1
O que vai acontecer aqui é o seguinte, o carrinho sai do repouso mas quando chega lá embaixo tem velocidade. Isso acontece por quê a energia mecânica envolvida no sistema se conserva e podemos usar a equação que iguala as energias inicial e final.
No looping o carrinho vai realizar um movimento circular, onde a força resultante é a força centrípeta que aponta para o centro da circunferência.
Usaremos esses dois conceitos pra resolver essa questão, a conservação de energia vai ajudar a gente a encontrar a velocidade no topo do looping e a força centrípeta pra encontrar a força que os trilhos fazem no carrinho.
Passo 2
Vamos pegar o ponto de onde o carrinho parte do repouso e o topo do looping, e fazer aqui a conservação de energia.
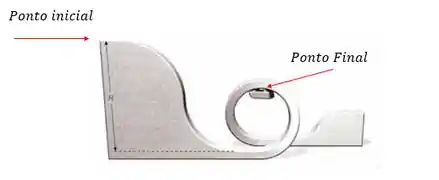
No ponto mais alto da montanha a energia mecânica será a inicial, e como não tem velocidade é somente a energia potencial.
No topo do laço, o carrinho terá energia cinética e potencial, nesse caso ele já perdeu alguma altura agora em relação ao chão tem altura de que é o diâmetro da trajetória.
Igualando as energias temos:
Substituindo , , e , temos:
Para descobrir a velocidade no ponto mais alto do laço, vamos usar a fórmula da energia cinética:
Passo 3
Agora que já sabemos a velocidade, podemos calcular a força que os trilhos exercem sobre o carrinho
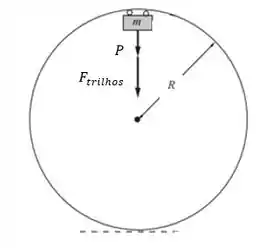
A força peso e a força dos trilhos apontam pra baixo nesse ponto, sendo assim podemos aplicar a segunda lei de newton pra relacionar a força centrípeta com as forças atuantes.
Como , temos:
Sendo assim temos:
Substituindo valores temos: