Um bloco de massa desce uma rampa partindo do repouso de altura tomando como referência a parte inferior da rampa. Após iniciar a descida, o bloco passa por um ponto localizado na rampa em uma altura com velocidade e por um ponto localizado na rampa em uma altura com velocidade . Ao chegar à parte inferior, o bloco encontra uma plataforma horizontal e continua se deslocando até tocar e comprimir de uma mola de constante elástica fixa na horizontal.
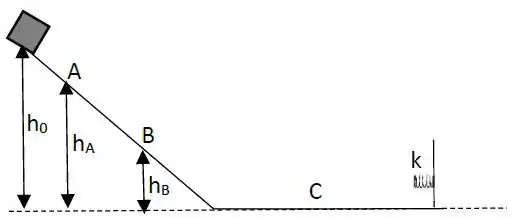
- Determine o trabalho realizado pela força gravitacional sobre o bloco para ir do ponto até o ponto em função de , e .
- Determine a altura em função de e .
- Determine a velocidade na parte em um ponto na plataforma antes de tocar na mola em função de e .
- Determine a compressão máxima da mola em termos , , e .
- Se a massa inicial fosse dobrada, valendo , a velocidade no ponto aumentaria, diminuiria ou continuaria o mesmo em relação a situação com a massa ?
Passo 1
Vamos lá! Como no item (a) ele quer o trabalho realizado pela força gravitacional em termos de e , vamos aplicar o teorema Trabalho-Energia Cinética
Passo 2
No item (c) queremos saber a altura em termos de e . Para isso podemos usar a conservação da energia.
A energia em é apenas potencial gravitacional
A energia no ponto A é potencial gravitacional e cinética
Igualando as duas, temos
Passo 3
No item (c), precisamos escrever a velocidade em termos de e . Para isso vamos usar a conservação da energia mecânica. Podemos imaginar que no ponto B a energia mecânica é cinética e potencial gravitacional, sendo assim
E no ponto é apenas cinética
Igualando temos
Passo 4
No item (d) queremos descobrir a compressão máxima da mola. Novamente usaremos a conservação da energia. Agora toda energia será armazenada na mola.
E a energia no ponto é
Igualando as energias, temos
Passo 5
No item (e) queremos saber o que acontece com a velocidade no ponto se a massa passar a ser .
Podemos usar a conservação da energia quando o bloco está parado a uma e cai até chegar ao ponto .
Portanto, a velocidade no ponto não dependerá da massa do bloco.