4) Considere o gráfico a seguir, onde a linha curva representa a energia potencial de uma partícula, que se movimenta em uma dimensão, e a linha reta, horizontal, a sua energia mecânica (ambas em Joules) em função da sua posição (em m).
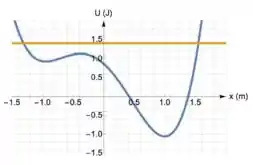
Sejam as afirmativas abaixo:
- O movimento da partícula possui dois pontos de retorno.
- A partícula tem velocidade máxima em
- A força que atua na partícula se anula nos pontos de interseção entre curvas de energia potencial e energia mecânica.
São VERDADEIRAS apenas:
(a) Todas
(b) e
(c)
(d)
(e)
Passo 1
Fala aí, galerinha!!
O problema nos deu um gráfico onde a gente consegue ver o comportamento da energia potencial e da energia mecânica de uma partícula se movimentando em uma dimensão. Antes da gente testar as afirmações que o problema nos deu, dá para a gente concluir algumas coisas desse gráfico que vão facilitar esse problema.
A primeira delas é que como a energia mecânica é uma linha reta horizontal, isso quer dizer que ela é constante ao longo do movimento. Quando temos isso, temos um sistema em que há conservação da energia mecânica, beleza? A gente também pode lembrar que a energia mecânica de um sistema é dado por:
Onde é a energia cinética.Bom, isso já nos ajuda um pouco. Tá vendo aqueles dois pontos em que o gráfico da energia potencial encosta no da energia mecânica? Nesse ponto temos:
Quando isso acontece, dizemos que esse ponto é um ponto de retorno. É um ponto em que a partícula para de se mover, adiquire energia potencial máxima e começa a voltar. As partes do gráfico fora desses pontos de retorno não podem existir pois teríamos:
Beleza? Então vamos ver as afirmações!!
Passo 2
A primeira afirmação nos diz que:
“O movimento da partícula possui dois pontos de retorno.”
Como vimos no passo anterior, temos dois pontos onde a energia mecânica é igual a energia potencial. Ou seja, temos dois pontos de retorno mesmo. Essa afirmação é verdadeira 😊
Passo 3
A segunda afirmação nos diz que:
“A partícula tem velocidade máxima em .”
Bom... Se olharmos no gráfico, em temos o menor valor da energia potencial. Como temos a conservação da energia mecânica:
Quando uma dessas energias diminui a outra tem que aumentar para manter aquela soma igual a um valor constante. Então neste ponto vamos ter o maior valor de . Como é dado por:
Teremos o maior valor de velocidade possível neste ponto! Essa afirmação é verdadeira 😊
Passo 4
A terceira afirmação nos diz que:
“A força que atua na partícula se anula nos pontos de interseção entre curvas de energia potencial e energia mecânica.”
Para entender melhor essa, a gente tem que lembrar que a força que atua na partícula tem uma relação com a energia potencial dada por:
Na prática, a força está relacionada com a inclinação da reta tangente à curva. Nos pontos de interseção entre as curvas, vemos que ainda existe uma reta tangente associada à curva . OU seja, existe uma força atuando na partícula neste ponto.Então essa afirmação é falsa!E aí resolvemos essa 😊 Vamos para a próxima??
Resposta
(d)