Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Conservação da Energia Mecânica

Ver Teoria
Exercício 311234567891011121314151617181920212223242526272829303233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Uma partícula de massa m   =   1   k g está sujeita a um potencial U x = - x 3 + 6 x 2 - 9 x + 1 , onde x é dado em metros e U em Joules, representado graficamente na figura.

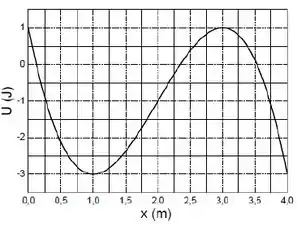
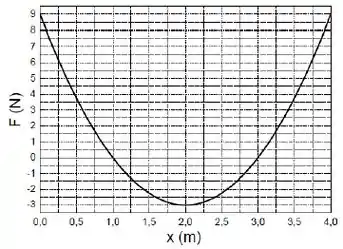
  1. Determine a força F(x) atuando na partícula e represente-a graficamente.
  2. Identifique os pontos de equilíbrio e classifique-os (estável ou instável).
  3. Em x   =   2 , a partícula é abandonada a partir do repouso. Em que direção e sentido a partícula passará a se mover? Qual é o módulo da força que atua nela neste ponto?
  4. Para a condição inicial do item (c), em que ponto a velocidade da partícula será máxima e qual será o seu valor?
  5. Para a condição inicial do item (c), quais serão, aproximadamente, os valores máximo e mínimo de x para essa partícula?

Passo 1

  1. Para encontrarmos a função da força, devemos derivar a energia em função de de x (multiplicando por - 1 a função da energia ,logo:

    2. F x = - U x d x = ( 3 x 2 - 12 x + 9 )   N

    Passo 2

  2. Os pontos de equilíbrio ocorrem quando F x = 0 , ou seja, precisamos determinar as raízes dos gráficos. Logo,

    3. x = 1   m   →   p o n t o   d e   e q u i l í b r i o   e s t á v e l

    x = 3   m   →   p o n t o   d e   e q u i l í b r i o   i n s t á v e l

    Passo 3

  3. Substituindo x = 2 na função da força, teremos:

    4. F 2 = 3 . 2 2 - 12.2 + 9 =   - 3 N

    Logo, sendo abandona na posição x = 2 a partícula se deslocará no sentido negativo do eixo x.

    E o módulo da força será F = 3 N .

    Passo 4

  4. Sendo a energia total a soma entre a energia cinética e a energia potencial, teremos:

    5. E x = U x + K ( x )

    Sabendo que o corpo parte do repousa em x = 2 , a energia total neste ponto é conservada para todos os pontos.

    E 2 =   - 1 J

    Sabemos que a energia cinética é máxima onde a energia potencial é mínima. Pelo gráfica, vemos a energia cinética é mínimo para x = 1 , assim:

    E 2 = E 1 = U 1 + K 1 ⇒   - 1 = - 3 + K ( 1 )  

    K 1 = 2 J

    Calculando a velocidade, teremos:

    K = m v 2 2   ⇒ v =   2 K m   ⇒ v = 2 . 2 1 = 2   m / s    

    Passo 5

  5. Para as condições da letra ( c ) a energia potencial gravitacional varia de - 1 J   a - 3 J   E < U .

Logo, o valor de x varia no intervalo:

0,25 < x < 2   m

Resposta

a )   F x = - U x d x = ( 3 x 2 - 12 x + 9 )   N

b )   x = 1   m   →   p o n t o   d e   e q u i l í b r i o   e s t á v e l

x = 3   m   →   p o n t o   d e   e q u i l í b r i o   i n s t á v e l

c )   F = 3 N     ( S e n t i d o   n e g a t i v o   d o   e i x o   x )

d )   v = 2   m / s

e )   0,25 < x < 2   m

Exercícios de Livros Relacionados

O cume do monte Everest está 8850m acima do nível do mar. (a) Qual seria a energia gasta por um alpinista de 90k g para escalar o monte Everest a partir do nível do mar, se a única força que tivesse q
Uma bola de 50g é lançada de uma janela com uma velocidade inicial de 8,0m / s e com um ângulo de 30 ° acima da horizontal. Usando a lei de conservação da energia, determine (a) a energia cinética da
Uma bola de neve de 1,50k g é atirada para cima em um ângulo de 34,0 ° com a horizontal e com uma velocidade inicial de 20,0m / s . (a) Qual é a energia cinética da bola? (b) De quanto varia a energia
Uma locomotiva com uma potência de 1,5M W pode acelerar um trem de uma velocidade de 10m / s para 25m / s em 6,0m i n . (a) Calcule a massa do trem. Determine, em função do tempo (em segundos), (b) a
b) Qual é a rapidez da bola ao chegar no chão