Um bloco de massa é liberado, com velocidade inicial , a uma altura . Desprezando a resistência do ar, o bloco desliza sobre um trilho sem atrito de acordo com a figura abaixo:
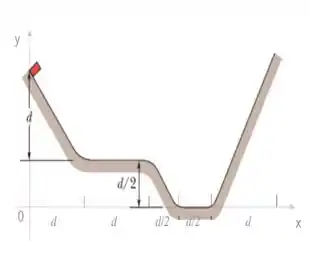
a) Calcule a velocidade do bloco ao chegar no segundo trecho plano do trilho.
(b) Determine a altura atingida pelo bloco no último trecho do trilho.
(c) Esboce, numa única figura, a energia cinética, a energia potencial gravitacional e a energia total do bloco durante percurso entre e 3d. Identifique no gráfico a posição do bloco em cada trecho.
(d) Considere que a superfície do primeiro trecho plano do trilho dissipe de energia do bloco devido ao atrito. Recalcule a altura que o bloco atingirá o último trecho do trilho nessa situação
Passo 1
Bem! Vamos começar! Bora entender o que está acontecendo... Pra isso, bora fazer um desenho...
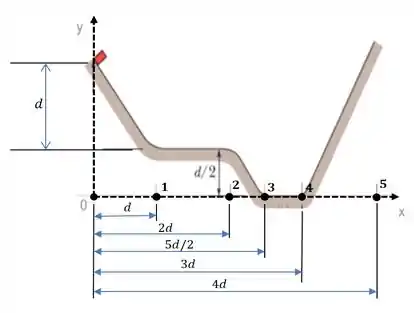
Que bela imagem, né não!?
Feito isso, vamos ao que interessa!
a) Nessa primeira letra, precisamos encontrar a velocidade do bloco ao chegar no segundo trecho plano do trilho.
Ou seja! Precisamos achar a velocidade do bloco quando ele chega naquele ponto que nomeamos de ! Ele é o começo do segundo trecho plano do trilho
Ora bolas! Vamos então recorrer a conservação da energia mecânica!
Chamando de a velocidade do bloco no começo do segundo trecho plano e de a velocidade inicial, temos que...
Como está na origem do nosso referencial, temos que . Logo, ficamos com:
Onde :
Substituindo os valores numéricos...
Passo 2
b) Em seguida, temos que determinar a altura atingida pelo bloco no último trecho do trilho, ou seja, a altura quando está em !
E como em , ele vai estar na altura máxima sem atrito, então a velocidade nesse ponto vai ser nula. Aplicando a conservação da energia mecânica, temos que...
Isolando e substituindo os valores numéricos...
Tamo indo bem, GUYS!
Passo 3
c) A próxima coisa a se fazer é esboçar, numa única figura, a energia cinética, a energia potencial gravitacional e a energia total do bloco durante percurso entre e 3d.
Bom! Essa sem dúvida! É a letra mais trabalhosa do exercício!
Isso porque pra plotar o gráfico com todas as energias! Vamos ter que analisar intervalo por intervalo por intervalo, isso pra obter o melhor gráfico possível!
No primeiro intervalo, que vai de até , a energia cinética aumenta um pouco ao passo que a energia potencial diminui.
No segundo intervalo de até , pela pista não ter atrito, as energia cinética e potencial em serão constantes.
E quando chega no terceiro intervalo, de até , o que acontece é que a energia potencial cai pra zero ao passo que a energia cinética cresce a ponto de igualar-se a energia mecânica total do sistema. Essas energia serão constantes no quarto intervalo, até ao ponto em que no quinto intervalo, a energia potencial sobe de novo até igualar-se à energia mecânica e a energia cinética cai pra zero!
Temos então, o seguinte gráfico abaixo,
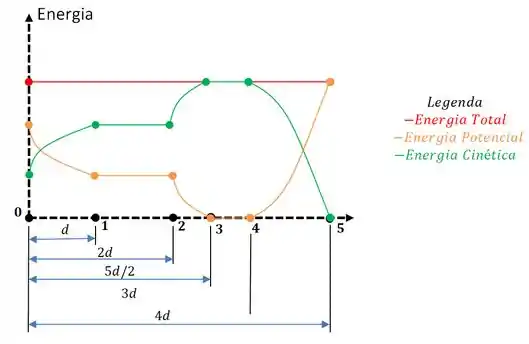
Passo 4
d) Por último, temos que recalcular a altura do item (b), considerando que a superfície do primeiro trecho plano do trilho dissipe de energia do bloco devido ao atrito.
O que temos que fazer então, é aplicar a conservação da energia mecânica subtraindo da energia mecânica inicial do bloco quando ele vai ser largado da pista... Mais ou menos, o seguinte...
Entendeu aí!
Isolando e substituindo os valores numéricos...
Pronto! Missão cumprida!
Terminamos aqui!
Resposta
a)
b)
c)
d)