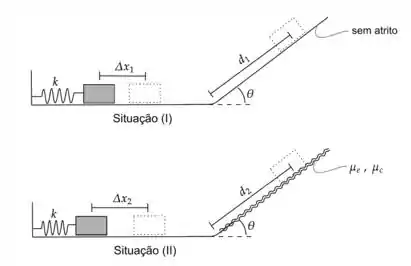
9) Um bloco de massa que se encontra encostado à extremidade livre de uma mola de constante elástica é impulsionado em direção a uma rampa inclinada de um ângulo após percorrer um trecho horizontal.
- Na situação , a mola está comprimida em e não existe atrito em nenhum dos dois trechos do percurso.
- Na situação , a mola está comprimida em e existe atrito apenas no trcho inclinado, cujos coeficientes estático e cinético são, respectivamente, e .
Sempre que necessário, considere a aceleração da gravidade no local.
- Na situação qual a velocidade do bloco imediatamente após se desprender da mola?
- Na situação , calcule a distância percorrida pelo bloco na rampa até atingir o repouso. Expresse sua resposta em termos de e .
- Na situação , represente o diagrama de forças que atuam no bloco quando ele está subindo na rampa inclinada.
- Na situação encontre , onde é a distância percorrida pelo bloco na rampa até atingir o repouso. Calcule qual deve ser o valor da compressão para que
Passo 1
Fala aí, galerinha!!
Esse problema tem duas situações. A primeira, como não tem atrito, vamos sempre pegar dois pontos do movimento e usar a conservação da energia mecânica:
Como temos trechos em que o bloco possui velocidade, trechos onde existem molas comprimdas e trechos em que o bloco atinge uma certa altura, é legal escrevermos a conservação da energia mecânica assim ó:
Onde é a energia cinética, é a energia potencial elástica e é a energia potencial gravitacional. Beleza?Na segunda situação, a única diferença é que na rampa existe atrito, então neste trecho (e somente nele) não dá para usar a conservação da energia mecânica do sistema. Mas não tem problema! Como nesse trecho a força de atrito vai realizar trabalho e a força peso também. Podemos usar o teorema trabalho-energia cinética nesse trecho e encontrar o que o exercícios nos pede.
Então vamos lá!!
Passo 2
a) O sistema começa com o bloco comprimindo a mola em uma distância . Neste ponto só temos a energia potencial elástica que é dada por:
Se adotarmos este ponto como o nível zero de altura do sistema, teremos, neste ponto, e , então a anergia mecânica é:
Agora, o outro ponto que escolhemos para analisar esse sistema é o ponto em que o bloco se solta da mola. Nesse ponto o bloco adquire uma velocidade e como a mola fica em seu ponto de equilíbrio nesse ponto, temos:
A gente percebe que o bloco não muda de altura em relação ao ponto inicial, então ainda temos , ou seja, a energia mecânica neste ponto é puramente cinética:
Como a energia mecânica se conserva nesse ponto temos:
Arrumando isso temos:
Passo 3
b) Agora o problema pede a distância, sobre a rampa, que o bloco percorre até parar. Então vamos comparar dois pontos. O ponto inicial, onde a mola estava comprimida e já vimos que a energia mecânica neste ponto é:
E o ponto final é dado pelo ponto mais alto que o bloco consegue chegar. Nesse ponto o bloco para, né? Então temos e como não há compressão de mola nesse ponto teremos:
Pera, quem é esse ? É a altura que o bloco consegue subir em relação ao ponto que marcamos como origem. Se olharmos essa figura aqui:
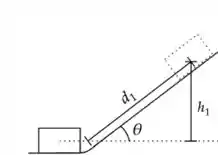
Temos a relação entre e dada por:
Então temos a energia mecânica no ponto mais alto dada por:
Usando a conservação da energia mecânica nos pontos que escolhemos temos:
Resolvendo para temos:
Passo 4
c) Agora temos a situação quando há atrito na rampa. Neste caso, quando o bloco está subindo, temos uma força de atrito que é contrária ao movimento de subida então temos o diagrama de forças assim ó:
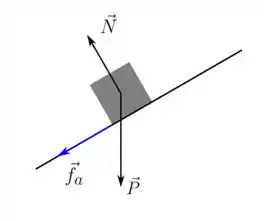
Onde é a força normal da superfície, é a força de atrito entre o bloco e a rampa e é a força peso.
Passo 5
d) O problema nos pede para calcular o trabalho da força de atrito para o bloco subir uma distância . O trabalho da força de atrito é dado por
O sinal de menos é porque a força é oposta ao deslocamento. Como o bloco está em movimento, a força de atrito é uma força de atrito cinético e é dada por:
Para calcular a normal, precisamos fazer a decomposição da força peso. Em nosso diagrama temos:
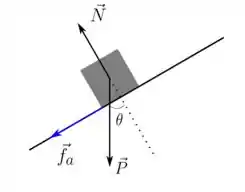
E percebemos que a força peso possui uma componente na direção da força normal dada por:
Como não há movimento nessa direção perpendicular à rampa temos:
Então o trabalho da força de atrito é dado por:
Passo 6
e) Nesse item ele tá pedindo uma distância até o bloco parar. Aqui a gente pode fazer assim: O bloco começa com a mola comprimida e chega na base com uma velocidade , certo? Só que nesse movimento a situação é igualzinha àquela que a gente fez no passo 2! Então a gente pode roubar aquela velocidade trocando o deslocamento da mola:
Quando o bloco sobe a rampa, tanto o atrito quanto a força peso realizam trabalho. Então podemos usar o teorema trabalho-energia cinética e escrever:
A variação da energia cinética é dada por:
Como a velocidade no início desse trecho é e no fim é zero, temos:
O trabalho da força de atrito nós já calculamos no passo anterior. Para uma distância temos:
O trabalho da força peso é dado por:
Pois somente a componente paralela ao movimento contribui. Olhando a decomposição que fizemos já para o peso, temos :
Com isso, o teorema trabalho-energia cinética nos dá:
Arrumando isso temos:
Passo 7
A última coisa que ele pede é para encontrar que faça com que . Bom, então a gente iguala essas duas distâncias que calculamos:
Simplificando um pouco temos:
Resolvemos essa 😊 Vamos para a próxima??
Resposta
Ei, a resposta está no passo a passo :)