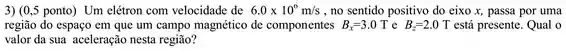
Passo 1
Primeira coisa que a gente precisa é entender que só a componente do campo magnético que é perpendicular vai fazer com que o elétron se mova.
Passo 2
Então, só a componente importa para gente. Ela faz um ângulo de com a velocidade , usando a fórmula da força magnética:
Dividindo essa força pela massa do elétron a gente encontra a aceleração:
Resposta
Exercícios de Livros Relacionados
Em um modelo pré-mecânica quântica para o átomo de hidrogênio, um elétron orbita em torno de um próton a um raio de 5,29 × 10 - 11m . De acordo com este modelo, qual é a magnitude do campo magnético n
Uma barra metálica de massa m desliza em um par de longos trilhos horizontais condutores, paralelos, separados por uma distância L e conectados a um dispositivo que fornece corrente constante I para o
Um próton está se movendo em uma região onde existe um campo magnético uniforme dado por B → = 10 i ^ – 20 j ^ + 30 k ^ m T . No instante t 1 , o próton possui uma velocidade dada por v → = v x i ^ +
Uma partícula alfa se move com uma velocidade v → de módulo 550 m / s em uma região onde existe um campo magnético B → de módulo 0,045 T . (Uma partícula alfa possui uma carga de + 3,2 × 10 - 19 C e u
Um elétron possui uma velocidade inicial de 12,0 j ^ + 15,0 k ^ k m / s e uma aceleração constante de 2,00 × 10 12 m / s 2 i ^ em uma região na qual existem um campo elétrico e um campo magnético, amb