Na figura abaixo, uma partícula descreve uma trajetória circular em uma região onde existe um campo magnético de módulo , cujo sentido é mostrado na figura. A partícula pode ser um próton ou elétron (a identidade da partícula faz parte do problema) e está sujeita a uma força magnética de módulo igual a .
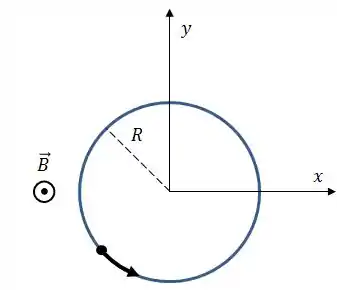
Determine:
A velocidade escalar da partícula;
Explicar qual partícula está girando em ;
O raio da trajetória;
O período do movimento;
Passo 1
A velocidade escalar da partícula;
A única força que está atuando sobre a partícula é a força magnética, que é dada por:
Aqui, como a partícula se movimenta somente no plano da página e o campo magnético é perpendicular ao plano da página, e serão sempre perpendiculares, isso significa que podemos reescrever a fórmula acima como:
Onde:
Onde corresponde à carga elementar, que é a carga deum próton ou um elétron. Como ainda não sabemos quem é essa partícula, vamos usar o valor positivo para calcular a velocidade.
Passo 2
Explicar qual partícula está girando em ;
A força magnética estará sempre apontando para dentro da trajetória. A velocidade é sempre tangencial e o campo magnético está sempre apontando para fora da página.
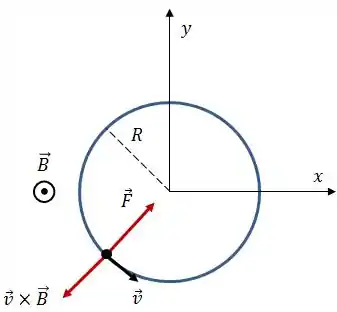
Para que esteja apontando para dentro da trajetória, de acordo com a regra da mão direita, é necessário que a partícula seja um elétron.
Passo 3
O raio da trajetória;
Como a partícula realiza uma trajetória circular, a força magnética (que mantém a partícula nessa trajetória) deverá ser igual à força centrípeta, logo:
Agora é só organizar isso pra chegar a uma expressão para o raio:
Onde a massa do elétron é aproximadamente .
Passo 4
O período do movimento;
Bom, já temos a velocidade e temos o raio, agora ficou tranquilo.
Resposta
A partícula é um elétron