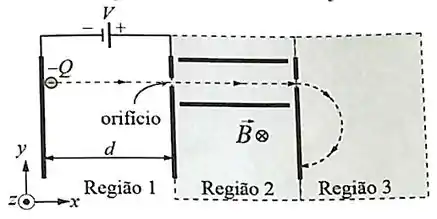
Um feixe de partículas com carga e massa é acelerado a partir do repouso através de uma diferença de potencial na região , e entra na região com uma gama de velocidade cuja direção é mostrada no diagrama. Há um campo magnético de módulo dirigido para dentro da página na região e um campo elétrico de módulo criado por placas paralelas carregadas na região 2. Com isso, algumas partículas passam pela região sem serem defletidas. Estas partículas entram na região , que contém somente um campo magnético de mesmo módulo e com a mesma orientação que na região . Determine:
(a) o módulo e a orientação do campo elétrico na região ;
(b) a velocidade com que as partículas entram na região ;
(c) o módulo da força magnética sobre as partículas na região ;
(d) o tempo de voo da partícula na região .
Passo 1
A força elétrica aplicada nas partículas deve ter orientação contrária e de mesmo módulo que a força magnética, para que as partículas não sejam defletidas.
As forças elétrica e magnética são dadas por:
Ou seja, a força magnética é orientada de cima para baixo. Para que as forças tenham sentidos opostos, a força elétrica deve ser orientada de baixo para cima. Isso significa que o campo elétrico, como o feixe possui carga negativa, deve ser orientado de cima para baixo.
Igualando as forças em módulo, temos que:
Passo 2
O valor da velocidade é obtido igualando as energias potencial e cinética:
Assim sendo,
Passo 3
A velocidade com que as partículas entram na região é a mesma da entrada na região , ou seja,
Passo 4
A força magnética na região é dada por:
Seu módulo será:
Passo 5
Na região , a trajetória das partículas será circular. Portanto,
onde é o raio da trajetória. Temos:
Passo 6
O tempo de voo será dado, portanto, por:
Resposta
(a)
(b)
(c)
(d)