Uma partícula de massa e carga , movendo-se no plano da página, é acelerada a partir do repouso através de uma diferença de potencial entre duas placas paralelas, como mostrado na região 1 da figura abaixo. A partícula passa por um orifício na placa da direita e penetra na região 2, onde há um campo magnético uniforme , perpendicular ao plano da página. Após descrever uma trajetória semicircular, a partícula atinge um detector. Em termos dos parâmetros dados e desprezando a ação da gravidade, determine:
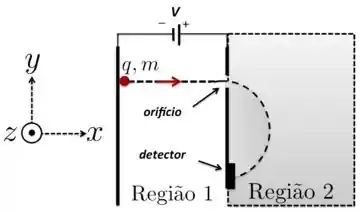
- O sinal da carga da partícula. Justifique.
- O sentido do campo magnético. Justifique.
- A velocidade da partícula ao entrar na região do campo.
- O vetor força exercida sobre a partícula pelo campo magnético no instante em que ela atinge o detector.
- A distância do orifício ao detector.
Passo 1
a) Como a partícula carregada está saindo do polo negativo para o polo positivo de uma bateria, seu sinal é negativo, ou seja, .
b) Agora, quando essa carga entra no região onde tem campo magnético, ela sofre uma força perpendicular à sua velocidade e que muda a sua direção. Como a força é dada por
e essa força “puxa” a partícula para baixo quando a partícula está exatamente no orifício, então, o campo magnético deve ser , ou seja, deve estar entrando no plano da página. Para verificar:
que mostra que a força sobre no orifício está para baixo.
FICA LIGADO: esse é o vetor força magnética EXATAMENTE NO ORIFÍCIO, porque embora a força tenha o mesmo módulo em toda a região 2, o vetor muda de direção e sentido ao longo do percurso de !!
Passo 2
c) Quando está na região 1, ela recebe uma energia através do potencial que a acelera levando-a de uma velocidade inicial zero até uma velocidade final com a qual ela entra na região 2.
A energia que tem é igual ao trabalho realizado pelo campo que tem na região 1 para levá-la até o orifício. Esse trabalho é igual à variação da energia potencial sobre :
em que é o potencial do ponto de partida e o potencial de chegada no ponto , onde está o orifício. Da figura, .
No entanto, esse trabalho deve ser igual à variação da energia cinética de . Portanto:
Passo 3
d) Como vimos, a força que sente quando está exatamente no ponto do orifício é:
Agora, à medida que entra na região 2, força magnética centrípeta puxa para dentro do círculo e, por isso, esse vetor vai mudando de direção dentro da região 2, mas tem sempre o mesmo módulo.
Quando chega no ponto no detector, a força tem sentido oposto do de entrada. Então, no detector teremos:
Passo 4
e) Para fechar, como a força centrípeta é a força magnética e essa força apenas muda a direção da velocidade de ao longo da trajetória, podemos associar o movimento de na região 2 ao movimento circular uniforme, vulgo MCU.
Utilizando o MCU, o raio da trajetória circular descrita por na região 2 é:
A distância do orifício até o detector é exatamente igual do diâmetro do círculo. Por isso, temos:
Resposta
- entrando na página;