USP, Sem Campus, Física 3, Listas de Física 3 - USP - Lista 1 - Lei de Coulomb, Campo Elétrico, Lei de Gauss, Questão 8a
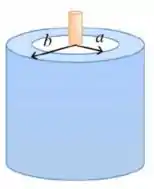
8) Um fio isolante muito longo (cor laranja) é colocado sobre o eixo de um cilindro metálico oco (cor azul), também muito longo. A densidade linear de carga do fio é , enquanto a densidade de carga por unidade de comprimento do cilindro é . (a) Qual a densidade de carga por unidade de comprimento nas superfícies interna e externa do cilindro, admitindo equilíbrio eletrostático?
Passo 1
Iae, como vai? Essa questão está um pouco complicada? Fique tranquilo que vamos tentar te ajudar. 😎👍
Nessa questão temos um fio infinito de densidade de carga por unidade de comprimento e envolta do fio há um cilindro oco também infinito com raio interno e raio externo e densidade de carga por unidade de comprimento.
Com essa situação, queremos saber qual é a densidade de cargas nas superfícies interna e externa do cilindro.
E aí, tem alguma ideia de como podemos fazer isso? 🤔
Para resolver esse problema, vamos lembrar de algumas propriedades da lei de Coulomb...
Já sabemos que cargas opostas se atraem e cargas com sinais iguais se repelem.
Não é mesmo? 😐
Passo 2
Agora vamos estudar o que acontece em uma seção transversal do conjunto fio-cilindro.
Como o fio em densidade e o cilindro tem densidade , a quantidade de cargas no cilindro por unidade de comprimento é o dobro do fio, ou seja, se o fio tiver cargas positivas e negativas, o cilindro terá cargas positivas e negativas.
Assim, e , então
Vamos desenhar o esquema...
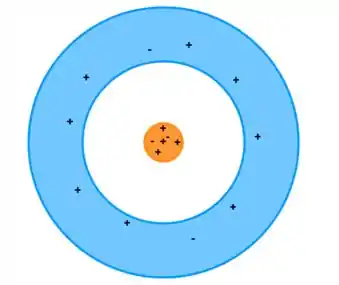
Porém, o que sabemos da lei de Coulomb é que cargas opostas se atraem e cargas iguais se repelem.
Dessa forma, como foi dito que o sistema está em equilíbrio estático, acontece que as cargas de maior número no fio e no cilindro, vão ocupar a maior área do objeto, ou seja, as cargas positivas do cilindro, vão ocupar a superfície externa pois assim elas conseguem ficar o mais espaçadas entre si. Ou seja
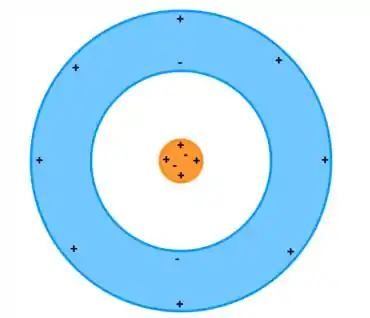
Tranquilo até aqui? 😁
Passo 3
Assim, relacionando a quantidade de carga com a densidade, vemos que se o fio tem e densidade , na superfície interna do cilindro há duas cargas negativas, então nessa superfície vamos ter uma densidade de carga
Agora na superfície externa do cilindro temos
E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí
