Um sistema a vácuo possui um pequeno vazamento de gás, cujos íons possuem carga e massa . Os íons escapam do vazamento na direção com velocidade de módulo . Para medir a intensidade do vazamento, aplica-se um campo magnético uniforme e estacionário de módulo e posicionamos um detector de partículas à direita da saída de gás no plano , conforme mostrado na figura abaixo.
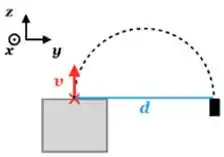
A que distância devemos posicionar o detector e que direção e sentido deve possuir o campo magnético para que os íons sejam detectados?
Escolha uma:
Passo 1
Vem comigo que a gente resolve essa juntos!
Nós temos que achar a distância e a direção e sentido do campo magnético.
Para achar a direção e sentido do campo, vamos usar a força de Lorentz ao nosso favor, ela é a força que uma carga com velocidade sofre na presença de um campo magnético, é dada por:
Do enunciado a gente sabe que está na direção a direção da força podemos deduzir através da figura.
Como os íons inicialmente sofrem um desvio na sua trajetória sempre para direita (direção ), temos que essa força inicialmente está nessa mesma direção.
Eu disse inicialmente, porque com o íon sofre esse desvio seu vetor velocidade muda de direção com isso a força também vai mudar de direção por conta do produto vetorial que temos na equação.
Agora para achar temos que usar nossos conhecimentos de mecânica, olhando a imagem a gente ver que a partícula faz um trajeto circular e para que esse trajeto aconteça precisamos ter uma força resultante que aponta para o centro dessa trajetória circular.
Essa força é a força centrípeta que tem o módulo dado por:
E quem faz esse papel no nosso problema é a força de Lorentz, assim:
Então basta isolarmos o que é o raio da trajetória e multiplicar por dois que teremos o diâmetro que é igual a .
Passo 2
Vamos primeiro encontrar a direção e o sentido do campo magnético, temos:
Sabemos que e que , assim:
Então o produto vetorial entre e tem que dar um vetor na direção , assim:
Para que esse produto dê um vetor na direção , temos que e só teremos componente na direção de .
Então tem direção .
Passo 3
Agora vamos calcular o módulo de para igualarmos com a força centrípeta, temos que:
Mas como e são perpendiculares temos que , asism:
Passo 4
Juntando tudo que a gente tem, ficamos com:
Isolando , temos:
Substituindo os valores que conhecemos, temos:
Então temos que:
Assim temos que:
Então a única opção verdadeira é a letra .
Finalizamos com sucesso!