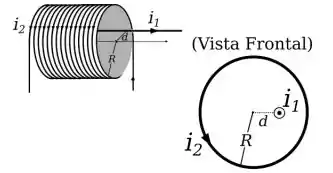
Um solenoide ideal de raio e densidade espiras por metro transporta uma corrente de intensidade . Um fio longo que transporta uma corrente de é posicionado paralelamente ao eixo do solenoide e a uma distância do seu eixo. Qual é a magnitude do campo magnético resultante em um ponto pertencente ao eixo do solenoide?
Passo 1
POW! Veja bem, temos duas fontes de campo magnético no problema: o fio longo, e; o solenoide.
A magnitude dos campos produzidos pelo fio e pelo solenoide é dada pelas expressões que achamos no nosso formulário:
“AH! Beleza! Então agora é só somar os dois valores”.
NãnãninaNÃO!
Afinal de contas, o campo magnético são vetores, então temos que fazer uma soma vetorial. Para isso, precisamos também da direção e sentido de todos os campos magnéticos (tanto do produzido pelo fio quanto do produzido pela espira).
Passo 2
De acordo com a regra da mão direita, podemos falar que o campo produzido pelo fio no centro do solenoide é...
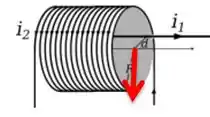
Ao passo que o campo magnético gerado pelo solenoide também pela regra da mão direita é...
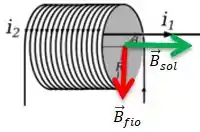
A soma vetorial desses dois vetores então será o campo magnético resultante no eixo da espira e o sentido pode ser dado pela regra do paralelogramo...
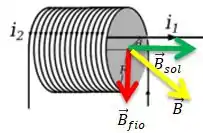
O valor do módulo de pode então ser dado por Pitágoras...
Então no nosso problema...
Passo 3
Bem... Agora é somente substituir todo mundo aí pelos valores dado no enunciado e ser feliz!
Simplificando...
Como e com uma calculadora em mãos...
Que é o mesmo que...
Como (micro)...
Resposta
Letra C.