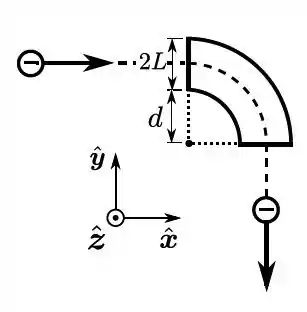
Um acelerador de partículas é projetado para desviar um elétron, de massa e carga , que incida horizontalmente, com velocidade inicial , para uma velocidade final . Assinale o campo magnético constante que permite que isso aconteça.

Aplicando a fórmula podemos descobrir o módulo do campo:

Agora a parada é descobrir o sentido dele. Sabemos que, como a partícula gira, o campo tem que produzir uma força centrípeta. Só, por favor, não esqueça que a carga tem valor negativo neste caso por se tratar de um elétron. Então você tem que achar o sentido como se ela fosse positiva e depois trocar ele pro oposto.

Pra achar o sentido de maneira bastante rápida podemos usar o macete desenvolvido na teoria/resumo/guia. Seja o unitário que dá o sentido de um vetor qualquer . Então temos:

Como a carga é negativa, o sinal do sentido troca:

Sabemos o sentido da força, pois a centrípeta tem sentido radial. Além disso também sabemos o sentido da velocidade em cada instante, pois ela é tangente à trajetória sempre. O que nós queremos é poder isolar o sentido do campo. Pelo macete do prisma:

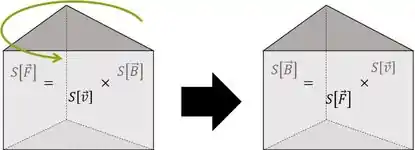
Então temos:

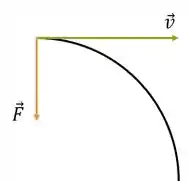
O sentido de pode ser encontrado se pegarmos qualquer instante da trajetória e calcularmos o produto vetorial, dado que sabemos que a força aponta pro centro:

Substituindo na equação:

Show, então temos nossa resposta:

Tranquilo? Se você não curtiu esse macete, você poderia alternativamente ficar chutando sentidos de até dar o sentido certo da força (sem esquecer do sinal da carga!), que é o que normalmente todo mundo faz. Não tem nenhum problema, até porque não são tantos sentidos assim.