UFMG – Fundamentos de Eletromagnetismo – P2 – Questão 4
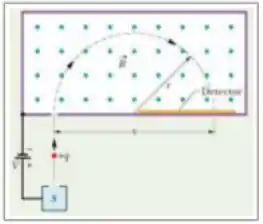
Considerando o espectrômetro de massa da figura, A) encontre a expressão literal para o raio em função dos valores de e ,supondo que a partícula esteja carregada com uma carga . B) Substitua , considere a massa e informe quanto vale .
Passo 1
Oi, tudo bem?
Essa questão parece complicada, mas vou ajudar você aqui! Vamos lá? Quando essa partícula entra na região de campo magnético, ela entra perpendicular ao campo!
Sendo assim, ela vai realizar uma trajetória circular, como está pontilhado no desenho do exercício!
Beleza?
Quando isso acontece, podemos dizer que a força magnética é igual a força centrípeta que a partícula sente:
E a força centrípeta depende do raio da trajetória! Então é daqui que vamos calcular o raio pedido!
Mas não temos a velocidade de entrada, então ainda não podemos sair substituindo! Sendo assim, precisamos de mais uma equação!
E é aqui que entra a conservação de energia! Toda energia potencial é utilizada para acelerar a partícula, dando a ela energia cinética! E é essa equação que vamos utilizar aqui!
Passo 2
A energia potencial é , e a energia cinética é , então, quando toda energia potencial é convertida em cinética temos o seguinte
E será que temos como substituir esse do lado esquerdo? Sim!
Temos sim! Lá do passo anterior:
Então podemos substituir em termos de e :
Tranquilo? Guarda essa expressão!
Passo 3
E essa velocidade? Ela não some nunca! Mas some sim! Da relação entre força magnética e força centrípeta
Podemos substituir essa velocidade na equação para o raio da trajetória que encontramos no passo anterior!
Encontramos o raio da trajetória em termos de e !
Passo 4
Agora com os valores dados, é só substituir:
, considere a massa :
Beleza? É isso! Espero ter ajudado!
