PARTE

Uma partícula carregada de massa e carga total penetra numa região do campo com campo magnético constante   através do ponto como indicado na figura abaixo. Ao entrar nessa região, a partícula apresenta uma velocidade de entrada , onde . Dentro dessa região, a partícula interage com o campo magnético e torna a sair no ponto , localizado a uma distância e com velocidade de saída igual a . Todos os vetores estão de acordo com o sistema de coordenadas apresentado na figura.

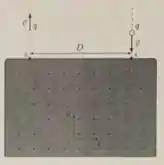
1. Qual é o valor (módulo) do campo magnético na região?
2. Qual foi o trabalho realizado pela força magnética?

PARTE

Como está representado na figura abaixo, uma corrente de intensidade percorre um fio dividido em três partes. Entre os pontos e , a corrente atravessa um fio retilíneo de comprimento entre os pontos e atravessa um semicírculo de raio e, por fim, entre os pontos e atravessa um outro fio retilíneo de mesmo comprimento .



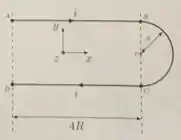
Utilizando explicitamente a lei de Biot-Savart e utilizando o sistema de referência fornecido:

3. Encontre o campo magnético (módulo, direção e sentido) causado pelo conjunto de fios retilíneos de comprimento no ponto .
4. Encontre o campo magnético   (módulo, direção e sentido) causado pelo semicírculo no ponto .

b) Como a força centrípeta, que no nosso caso aqui é a força magnética, é sempre perpendicular ao deslocamento da partícula, ela não realiza trabalho sobre a partícula carregada. Como vimos, existe aceleração centrípeta por causa da variação da direção da velocidade.

Portanto, a força magnética não realiza trabalho.

c) Para resolvermos este item, vamos dar uma olhada na figura abaixo. Nela, a gente representa os eixos que o problema fornece, mas, para facilitar, colocamos o fio superior da figura do problema na vertical. O campo gerado pelo fio superior estará entrando no plano da página, assim como o campo gerado pela corrente que passa no fio de baixo. Por isso, basta calcular o campo produzido por um dos fios e multiplicar por 2.

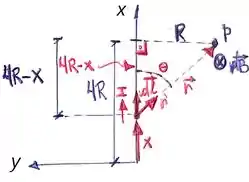
O campo magnético   gerado por quando ela passa no comprimento   do fio é dado por

em que  sempre aponta na direção e sentido da corrente naquele ponto e o vetor unitário  sempre aponta de até o ponto onde queremos calcular o campo. Como mostra a figura, o ângulo entre   e  é , de maneira que produto vetorial acima fica

sendo que aparece por causa da regra da mão direita.

Olhando para a figura, vemos que . Substituindo em   e depois integrando

Para resolvermos essa integral, podemos trocar as variáveis fazendo: , o que vai dar . Fazendo isso, vai ficar assim

que a gente resolveu dando consultando alguma tabela de integrais.

Agora, o campo no ponto devido aos dois fios será o dobro do campo acima

d) Pela regra da mão direita, o campo magnético gerado por quando ela percorre o semicírculo (SC) está entrando no plano da página e é perpendicular a ela. Nesse caso, o módulo do campo magnético será a metade do campo gerado por um círculo. Portanto, o vetor campo magnético   devido ao semicírculo será igual a

NO ENTANTO, PORÉM, TODAVIA...o problema pede para usarmos explicitamente a lei de Biot-Savart para chegar no vetor acima. Então, bora lá...

O elemento de comprimento  é sempre perpendicular ao semicírculo em todos os seus pontos. Por isso, o vetor unitário  é sempre perpendicular a  e a distância de todos esses elementos até o ponto é igual ao raio . Isso simplifica bastante as contas na lei de Biot-Savart:

Agora, também temos que  . Substituindo na expressão e depois integrando, a gente vai ter o seguinte:

Isso concorda com o que discutimos no começo do item: o campo magnético devido ao semicírculo no ponto é igual à metade do campo que seria gerado pelo círculo em .