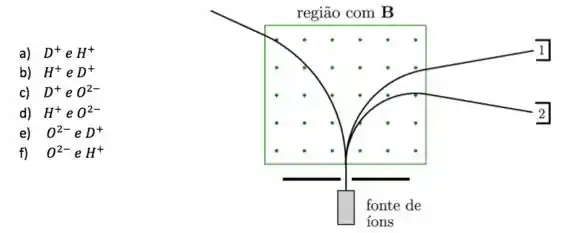
Em um espectrômetro de massa, um feixe de íons emitido por uma fonte atravessa uma região de campo magnético uniforme e estacionário, como mostrado na figura abaixo. Esse sistema é utilizado para determinar a quantidade de água pesada (, onde representa um átomo de deutério) que há na água do mar. Como resultado da ionização, separa-se apenas os íons , e , que são, então, acelerados de forma a entrarem na região de campo magnético com a mesma velocidade inicial. Sabendo que as massas dos átomos , e , valem 1, 2 e 16 u.m.a, respectivamente, e que a massa do elétron pode ser desprezada em confronto com as massas do próton e do nêutron, podemos afirmar que os íons coletados nos detectores 1 e 2, são, respectivamente:
Passo 1
Esse problema se refere a partículas carregadas que possuem mesma velocidade inicial ao entrarem em uma região onde há um campo magnético. Esse campo é o mesmo em toda a região e é sempre perpendicular à velocidade das partículas em discussão.
A força que atua em uma partícula carregada com velocidade que está em um campo magnético é dada por
em que é um produto vetorial. Se a carga for positiva, então a força terá o mesmo sentido do produto vetorial. Se for negativa, terá o sentido contrário.
Como a velocidade da carga é sempre perpendicular ao campo, o módulo da força que ela sente é
Como a força depende do produto vetorial, ela é sempre perpendicular a e a e tem sentido e direção sempre apontando para dentro da curva que cada partícula descreve.
Essa força, portanto, não altera a velocidade das partículas carregadas, mas apenas a direção e sentido de suas velocidades.
Passo 2
Uma vez vimos essas características gerais sobre a força em cada carga, precisamos agora conectá-las ao movimento circular uniforme (MCU). Por quê?
Pois no MCU, as partículas descrevem órbitas circulares e a força centrípeta que atua nelas muda apenas a direção e sentido de suas velocidades, sem alterar seus módulos. A mesma coisa acontece com os íons da questão que estamos resolvendo.
No nosso caso, a força magnética é que faz o papel da força centrípeta. Portanto, podemos escrever
A partir dessa expressão, vemos que o raio da trajetória de cada partícula carregada é dado por
Note que partícula carregada descreverá uma curva com raio em um sentido ou noutro dependendo do sinal de sua carga.
No caso do problema, duas cargas são positivas, e , e, portanto, descrevem uma curva no mesmo sentido. A curva descrita para a esquerda na figura é, então, da carga negativa .
Passo 3
Agora, para diferenciar quais partículas atingem os detectores 1 e 2, precisamos verificar qual das massas é maior, já que ambas e possuem mesma velocidade e mesma carga.
Já que o raio é diretamente proporcional à massa, aquela que possuir a maior massa, descreverá uma curvatura maior.
Concluímos, então, que atingirá o detector 1 e o detector 2.
Resposta
Portanto, a letra a) é a resposta correta.