UFF – Física 2 – Provas Antigas – P3 – 2022.1 – Questão 2
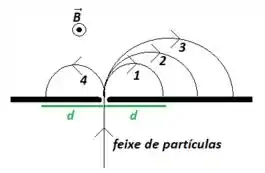
Considere a trajetória das partículas 1, 2, 3 e 4 através de um espectrômetro de massa, conforme ilustrado na figura. Considere também que todas as partículas entram no espectrômetro com a mesma velocidade e que as partículas possuem carga . Ordene em ordem decrescente estas partículas de acordo com suas massas.
A) .
B) .
C) .
D) .
E) .
Passo 1
Eaee!!! Belezinha? Olha.. basicamente nessa questão temos que saber que, para todas as 4 partículas, a velocidade, a carga e o campo são os mesmos!
No entanto, a questão nos pede para classificarmos em ordem decrescente as massas das partículas.
Aí eu te pergunto: Como podemos relacionar a massa com o campo magnético???
Pois bem, vamos lembrar da seguinte formulazinha:
Agora vamos lá!!
Passo 2
Vamos sempre colocar na cabecinha que a velocidade, as cargas e o campo são os mesmos e que todas as partículas estão submetidas a mesma força.
Lembrando da 2ª Lei de Newton, temos que . Assim, para que a força permaneça constante, campos de massas maiores experimentarão acelerações menores e vice-versa!
Passo 3
Consequentemente, observando a figura, vemos que a massa das partículas 1 e 4 devem ser iguais (porém com cargas diferentes).
Além disso, a massa da partícula 1 é menor que a da partícula 2, que é menor que a da 3, devido à diferença entre o tempo das trajetórias.
Assim, temos que:
Entendeu direitinho? Responde aee ;)
Resposta
D) .