No esquema da figura 1 estão representadas uma esfera compacta de material isolante de raio e uma casca condutora, concêntrica com ela, de raio interno e raio externo . A esfera isolante está carregada uniformemente com densidade volumétrica de carga . A casca condutora tem carga total nula.

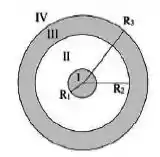
1. Suponha agora que a casca condutora é retirada e em seu lugar colocamos duas cascas esféricas isolantes, de espessuras desprezíveis, de raios e com a mesma distribuição de carga que havia no condutor. Qual o vetor do campo elétrico nas regiões ?

Bom... primeiramente para a região , onde .

Desenhando uma gaussiana esférica concêntrica com o isolante, temos que o campo elétrico é dado por:

Ou seja, não houve alteração no valor. Isso se deve ao fato de que não houve mudança na organização das cargas do isolante.

Para a região , temos que, colocando a gaussiana externa ao isolante e interna ao condutor:

Onde é a carga total.

Ou seja, não houve alteração no valor. Isso se deve ao fato de que não houve mudança na organização das cargas do isolante.

Para a região :

Nesta região, onde a casca condutora foi substituída por duas cargas isolantes, percebe-se que, como estas apresentam a mesma distribuição de cargas do condutor, a casca isolante interna de raio terá carga .

Por outro lado, a casca externa de raio terá carga .

Dessa forma, tem-se o seguinte esquema:

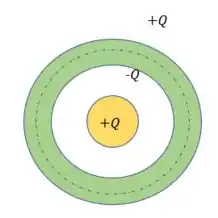
Inserindo-se a gaussiana entre as cascas de raio e , vemos que esta engloba uma carga total nula, visto que ela contém a esfera isolante de carga e a casca isolante de carga .

Dessa forma, pela Lei de Gauss:

Para a região :

Nessa região, colocando a gaussiana externa ao sistema, vemos que:

Entendeu direitinho? Responde aee ;)